背景 有限马尔可夫模型,即有限的状态间可通过有限的动作进行转移,并且转移情况只与上一个情况有关。本文将状态空间记为 \(\mathcal{S}\) ,动作空间记为 \(\mathcal{A}\) ,其笛卡尔积 \(S\mathcal \times \mathcal A\) 即为状态-动作空间。用 \(\mathcal{T}(s'\mid s,a)\) 表示在 \(s\) 状态下采取动作 \(a\) 后转移到 \(s'\) 状态的概率。
此外,每一次转移还附带一个收益 \(r(s, a)\) 。需要注意的是,如果存在终止环境 \(t\) ,应该把 \(r(t, \cdot)\) 均设为 0,即拒绝在终止状态进行行动。
在上述的模型上,强化学习要找到一个策略 \(\pi(a|s)\) 表示在状态 \(s\) 下采取状态 \(a\) 的概率。根据 \(\pi\) 可以定义状态-动作估价函数:
\[ \begin{equation} Q^\pi(s_0,a_0)=r(s_0,a_0)+\sum\limits_{i=1}^{\infty}\gamma^i\mathbb E_{s_i,a_i\mid s_0,a_0,\pi}[r(s_i,a_i)],\gamma \in(0, 1) \end{equation} \]
利用状态-动作函数,我们可以评估策略 \(\pi\) :
\[ \begin{equation} \eta(\pi)=\mathbb E_{s\sim \xi, a\sim \pi(s)}[Q^\pi(s,a)] \end{equation} \]
其中 \(\xi\) 表示初始环境分布。
状态-动作估值函数满足贝尔曼方程:
\[ \begin{equation} Q^\pi(s,a)=r(s,a)+\gamma \mathbb E_{s'\sim\mathcal T,a'\sim\pi}[Q^\pi(s',a')] \end{equation} \]
已经证明,对于给定的 \(\pi\) ,可以通过迭代上式的方法得到正确的 \(Q^{\pi}\) 。
强化学习的目的,是学习最优的 \(\pi^*\) :
\[ \begin{equation} \pi^*=\operatorname*{argmax}\limits_\pi \eta(\pi) \end{equation} \]
已经证明,最优的 \(\pi^*\) 满足最优贝尔曼方程:
\[ \begin{align} Q^*(s,a)&=r(s,a) + \gamma\mathbb E_{s'\sim\mathcal T,a'\sim\pi^*}[Q^*(s',a')]\\ &= r(s, a) + \gamma \mathbb E_{s'\sim\mathcal T}\max_{a'}Q^*(s',a') \end{align} \]
已有的 \(\pi^*\) 求解方法是根据策略提升定理,迭代以下步骤:
\[ \begin{equation} \pi(a|s) \leftarrow \left \{ \begin{aligned} 1,\ &a = \operatorname*{argmax}_aQ^\pi(s, a) \\ 0,\ &\text{otherwise} \end{aligned}\right. \end{equation} \]
本文将从线性代数的角度出发,重新推导以上结果,并且给出一种新的策略优化方法。
符号与约定 上述函数都可以写成矩阵的形式:
\[ \begin{aligned} &\mathcal T \in \mathbb R ^{|\mathcal S \times \mathcal A|}\times\mathbb R ^{|\mathcal S|},& & [\mathcal T]_{(s,a),s'}=\mathcal T(s'\mid s,a)\\ &r \in \mathbb R ^{|\mathcal S \times \mathcal A|},& & [r]_{(s,a)}=r(s,a)\\ &q^\pi \in \mathbb R ^{|\mathcal{S\times A}|}, & & [q^\pi]_{(s,a)}=Q^\pi(s,a) \\ & \pi \in \mathbb R ^{|\mathcal {S\times A}| }, & &[\pi]_{(s,a)}=\pi(a\mid s) \\ & \xi \in \mathbb R ^{|\mathcal S|}, & & [\xi]_{s}=P(s_0=s) \end{aligned} \]
为了表示方便,记 \(E \in \mathbb R ^{|\mathcal S \times \mathcal A|}\times\mathbb R ^{|\mathcal S \times A|}\) 为矩阵 \(\mathcal T\) 的一个扩展,满足 \([E]_{(s,a),(s',a')}=[\mathcal T]_{(s,a),s'}\) 。\(\varepsilon \in \mathbb R^{|\mathcal{S \times A}|}\) 为向量 \(\xi\) 的一个扩展,满足 \([\varepsilon]_{(s,a)}=[\xi]_s\) 。
策略评估的矩阵形式 迭代解法 贝尔曼方程,即 \((3)\) 式,可以写成如下形式:
\[ \begin{equation} \begin{bmatrix} q^\pi \\ 1 \end{bmatrix} = \begin{bmatrix} \gamma E\operatorname{diag}(\pi) & r \\ & 1 \end{bmatrix}\begin{bmatrix} q^\pi \\ 1 \end{bmatrix}\end{equation} \]
\([q^\pi,1]^\text T\) 是 \(|\mathcal{S \times A}|+1\) 维的向量。
将中间转移矩阵记为 \(A\) 。由于 \(A-I\) 的最后一行为空,所以 \(|A-I|=0\) ,即 \(A\) 的一个特征值为 1 。
对任意 \(q\) 迭代 \((8)\) ,即:
\[ \begin{equation} \begin{bmatrix} q_n \\ 1 \end{bmatrix} = A\begin{bmatrix} q_{n-1} \\ 1 \end{bmatrix}\end{equation} \]
下面证明 \(\lim\limits_{n \to \infty} q_n = q^\pi\) :
证明:
设 \(q_n = q^\pi + r_n\) ,则:
\[ \begin{aligned} &&\begin{bmatrix} q^\pi + r_n\\ 1 \end{bmatrix} &= A^n \begin{bmatrix} q^\pi + r_0\\ 1 \end{bmatrix} \\ &&&= A^n \begin{bmatrix} q^\pi\\ 1 \end{bmatrix} + A^n \begin{bmatrix} r_0\\ 0 \end{bmatrix} \\ &&&= \begin{bmatrix} q^\pi + (\gamma E \operatorname{diag}(\pi))^n r_0\\ 1 \end{bmatrix}\\ &\therefore&r_n&=(\gamma E \operatorname{diag}(\pi))^n r_0 \\ &&\Vert r_n\Vert_\infty &\le \Vert \gamma E \operatorname{diag}(\pi)\Vert_\infty^n \cdot \Vert r_0\Vert_\infty \end{aligned} \]
注意到 \([\gamma E\operatorname{diag}(\pi)]_{(s,a),(s',a')}=\gamma P(s',a'\mid s,a)\) ,因此其行和为 \(\gamma < 1\) 。所以:
\[ \begin{aligned} &&\lim_{n \to \infty} \Vert r_n\Vert_\infty &= 0\\ &\therefore&\lim_{n \to \infty} r_n &= 0\\ &\therefore&\lim_{n \to \infty} q_n &= q^\pi \end{aligned} \]
证毕。
封闭解法 根据谱半径的性质:
\[ \rho[\gamma E \operatorname{diag}(\pi)] \le \Vert \gamma E\operatorname{diag}(\pi) \Vert_\infty=\gamma < 1 \]
所以 \(\gamma E \operatorname{diag}(\pi)\) 的所有特征值大小都小于一。则:\(|\gamma E\operatorname{diag}(\pi)-I| \ne 0\) ,
又由于 \([q^\pi,1]^\text T=A [q^\pi,1]^\text T\) ,有:
\[ \begin{align} q^\pi &= \gamma E\operatorname{diag}(\pi)q^\pi + r \\ q^\pi &= (I-\gamma E\operatorname{diag}(\pi))^{-1}r \end{align} \]
在实践中,注意到 \(I-\gamma E\operatorname{diag}(\pi)\) 是极为稀疏的,只有至多 $ 2|S A|$ 个元素,可以利用稀疏性优化矩阵求逆。
策略优化 将 \((2)\) 式重写,得到:
\[ \begin{equation} \eta(\pi)=\pi^\text T\operatorname{diag(\varepsilon)}q^\pi \end{equation} \]
注意 \(\pi\) 是有限制的:\(\forall s,\sum_a{\pi_{s,a}}=1\) 。不能直接优化。
考虑维护一个无限制的 \(\pi'\) ,令 \(\pi_{(s,\cdot)}=\operatorname{Softmax}(\pi'_{(s,\cdot)})\) ,即对每个状态的不同动作进行 Softmax 操作。这样,问题就转化为了对于 \(\pi'\) 的无约束优化问题。本文实现了一些常见的无约束优化方法。
基于梯度的优化 记 \(I-\gamma E\operatorname{diag}(\pi)=M\) 。要最大化 \(\eta(\pi)\) ,考虑计算 \(\frac{\partial \eta}{\partial\pi}\) :
\[ \begin{equation} \frac{\partial \eta}{\partial\pi} = \operatorname{diag}(\varepsilon)q + (M^{-1}E)^\text T \operatorname{diag}(\varepsilon)\pi \end{equation} \]
\(\partial \pi'\) 可以由 \(\partial \pi\) 反向传播得到。基于此,我们可以采用 SGD、Adam 等方法优化 \(\pi'\) 。带动量的优化算法亦可应用。
由于 \((12)\) 式封闭的形式,牛顿法亦可应用,但是其形式过于复杂,没有实践意义。拟牛顿法也与牛顿法有相近的问题,不适合直接优化。
非梯度的优化 各种数值优化的方法都可以引用。通过实践,我们发现模拟退火算法表现较好。
此外,根据策略提升定理直接对 \(\pi\) 进行优化也是可行的。
实验与讨论 我们选取 grid-world 这一经典背景,在 \(n\times m\) 的网格中要求智能体从任意一格开始,沿网格走到右下角。每经过一格都有一个代价 \(c_{i, j}\) ,智能体需要最小化总代价。这是一个最短路问题,所以我们可以方便地判断智能体的行动是否最优。
下面给出环境模拟代码:
simulator.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 import numpy as npimport randomimport timefrom queue import PriorityQueueclass Simulator : def __init__ (self, n: int , m: int ) -> None : self .n, self .m = n, m self .stateNums = n * m self .map = np.abs (np.random.randn(n, m)) self .dis = np.zeros((n, m)) + 1e9 self .actionMap = [ { "dx" : 1 , "dy" : 0 }, { "dx" : -1 , "dy" : 0 }, { "dx" : 0 , "dy" : 1 }, { "dx" : 0 , "dy" : -1 } ] self .alpha = 1 self ._dijkstra() self .actionNums = len (self .actionMap) def _dijkstra (self ) -> None : pq = PriorityQueue() pq.put((0 , (self .n - 1 , self .m - 1 ))) while not pq.empty() : now = pq.get() d, (x, y) = now if self .dis[x, y] != 1e9 : continue self .dis[x, y] = d for move in self .actionMap : tx, ty = x + move["dx" ], y + move["dy" ] if self ._check(tx, ty) and self .dis[tx, ty] == 1e9 : pq.put((d + self .map [x, y], (tx, ty))) def _check (self, x: int , y: int ) -> bool : return ( x >= 0 and x < self .n and y >= 0 and y < self .m ) def _state (self ) -> np.ndarray : state = np.zeros((self .n, self .m)) state[self .x, self .y] = 1 return state.reshape(-1 , self .n, self .m) def _move (self, x: int , y: int , move ) : tx, ty = x + move["dx" ], y + move["dy" ] if (self ._check(tx, ty)) : return tx, ty else : return x, y def step (self, action: int ) -> tuple : if random.random() > self .alpha : action = random.randint(0 , self .actionNums - 1 ) self .x, self .y = self ._move(self .x, self .y, self .actionMap[action]) state = self ._state() reward = -self .map [self .x, self .y] terminated = self .x == self .n - 1 and self .y == self .m - 1 self .turns += 1 if self .turns > self .n * self .m : reward += -self .dis[self .x, self .y] terminated = True return state, self .x, self .y, reward, terminated def start (self ) -> np.ndarray : self .x = random.randint(0 , self .n - 2 ) self .y = random.randint(0 , self .m - 2 ) self .turns = 0 return self ._state(), self .x, self .y def _calc (self, x: int , y: int , a: int ) : return (x * self .m + y) * self .actionNums + a def state (self ) -> tuple : E = np.zeros((self .stateNums * self .actionNums, self .stateNums * self .actionNums)) r = np.zeros((self .stateNums * self .actionNums, 1 )) for x in range (self .n) : for y in range (self .m) : for a in range (self .actionNums) : move = self .actionMap[a] tx, ty = self ._move(x, y, move) if not (x == self .n - 1 and y == self .m - 1 ) : r[self ._calc(x, y, a)] -= self .map [tx, ty] for tta in range (self .actionNums) : E[self ._calc(x, y, a), self ._calc(tx, ty, tta)] += 1 return E, r
接下来,我们实现了基于本文给出的线性代数背景的智能体实现代码。其中实现了模拟退火、SGD、策略提升等多种优化算法:
agent.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 from simulator import *import matplotlib.pyplot as pltfrom math import *import osimport torchclass Agent : def __init__ ( self, n: int , m: int , gamma: float = 0.9999 , ) -> None : self .n, self .m = n, m self .simulator = Simulator(n, m) self .S = n * m self .A = self .simulator.actionNums self .gamma = gamma self .E, self .r = self .simulator.state() self .E = torch.from_numpy(self .E).type (torch.FloatTensor) self .r = torch.from_numpy(self .r).type (torch.FloatTensor) self .pi: torch.Tensor = torch.zeros((self .S, self .A)).type (torch.FloatTensor) self .optimizer = torch.optim.SGD([self .pi], lr=1e-3 , momentum=1e-3 ) def eval (self, pi: torch.Tensor ) -> torch.Tensor: PI = torch.softmax(pi, -1 ).view(-1 , 1 ) q = torch.inverse( torch.eye(self .S * self .A) - self .gamma * self .E @ torch.diag(PI.view(-1 )) ) @ self .r return PI.T @ q def test (self ) : state, x, y = self .simulator.start() score, bestScore = 0 , - self .simulator.dis[x, y] while True : action = torch.argmax(self .pi[x * self .m + y]) state, x, y, reward, terminated = self .simulator.step(action) score += reward if terminated : self .dis.append(float (bestScore - score)) break def SA (self, tempInit, epochs ) : self .pi.requires_grad = False for i in range (epochs) : temp = tempInit / (i + 1 ) dpi = self .pi + torch.rand_like(self .pi) y = self .eval (self .pi).item() ty = self .eval (dpi).item() if y < ty or random.random() < exp((ty - y) / temp): self .pi = dpi if i % 50 == 0 : self .test() def SGD (self, epochs: int ) : self .pi.requires_grad = True for i in range (epochs) : self .optimizer.zero_grad() eta = -self .eval (self .pi) eta.backward() self .optimizer.step() if i % 32 == 0 : self .test() def policyImprove (self, epochs: int ) : self .pi.requires_grad = False q = self .r for i in range (epochs) : PI = self .pi.view(-1 , 1 ) q = torch.inverse( torch.eye(self .S * self .A) - self .gamma * self .E @ torch.diag(PI.view(-1 )) ) @ self .r tq = q.view(self .S, self .A) self .pi = (tq == tq.max (axis=1 , keepdims=True )[0 ]).type (torch.FloatTensor) self .pi /= torch.sum (self .pi, dim=-1 , keepdim=True ) if True : self .test() def train (self, tempInit: float = 1.0 , SAepochs: int = 0 , SGDepochs: int = 0 , PIepochs: int = 0 ) -> None : self .loss, self .dis = [], [] simParam = "%dx%d-alpha%.1f" % (self .n, self .m, self .simulator.alpha) modelParam = "gamma%.4f-fixPolicyImprove-%d-A-Learning" % ( self .gamma, PIepochs ) self .policyImprove(PIepochs) self .SA(tempInit, SAepochs) self .SGD(SGDepochs) os.makedirs(simParam, exist_ok=True ) plt.plot(range (len (self .dis)), self .dis) plt.savefig("%s/%s-dis.png" % (simParam, modelParam)) plt.close() plt.plot(range (len (self .dis[-32 :])), self .dis[-32 :]) plt.savefig("%s/%s-lastdis.png" % (simParam, modelParam)) plt.close() if __name__ == '__main__' : agent = Agent(30 , 30 ) agent.train(PIepochs=256 )
另外,我们一并实现了传统的 Q-Learning 算法如下:
agent-Q.py
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 from simulator import *import matplotlib.pyplot as pltfrom math import log2import osclass Agent : def __init__ ( self, n: int , m: int , gamma: float = 0.9999 , initAlpha: float = -0.1 , finalAlpha: float = -0.1 , exploreNums: int = 2 ** 16 , testRoundNums: int = 1 , ) -> None : self .n, self .m = n, m self .simulator = Simulator(n, m) self .Q = np.random.randn(n, m, self .simulator.actionNums) self .gamma = gamma self .initAlpha = initAlpha self .finalAlpha = finalAlpha self .alpha = initAlpha self .exploreNums = exploreNums self .testRoundNums = testRoundNums def train (self ) : iterNums = 0 state, x, y = self .simulator.start() score, bestScore = 0 , - self .simulator.dis[x, y] round = 0 loss = [] while round < 4096 : action = random.randint(0 , self .simulator.actionNums - 1 ) if random.random() > self .alpha or round % self .testRoundNums == 0 : action = np.argmax(self .Q[x, y, :]) nextState, tx, ty, reward, terminated = self .simulator.step(action) iterNums += 1 score += reward self .Q[x, y, action] = reward + (1 - int (terminated)) * self .gamma * np.max (self .Q[tx, ty, :]) if iterNums < self .exploreNums : self .alpha -= (self .initAlpha - self .finalAlpha) / self .exploreNums if terminated : if round % self .testRoundNums == 0 : loss.append(float (bestScore - score)) round += 1 state, x, y = self .simulator.start() score, bestScore = 0 , - self .simulator.dis[x, y] else : state, x, y = nextState, tx, ty plt.plot(range (len (loss)), loss) os.makedirs("%dx%d-alpha%.1f" % (self .n, self .m, self .simulator.alpha), exist_ok=True ) plt.savefig( "%dx%d-alpha%.1f/gamma%.4f-4096-Q-Learning.png" % ( self .n, self .m, self .simulator.alpha, self .gamma ) ) plt.close() plt.plot(range (32 ), loss[-32 :]) plt.savefig( "%dx%d-alpha%.1f/gamma%.4f-4096-Q-Learning-last.png" % ( self .n, self .m, self .simulator.alpha, self .gamma ) ) plt.close() if __name__ == '__main__' : agent = Agent(30 , 30 ) agent.train()
实验结果用图表展示。每迭代一段时间,就会进行一次测试,即从随机初始位置开始让智能体与模拟器交互,记录智能体所花费代价与最短代价的差值。差值越小,智能体越优。
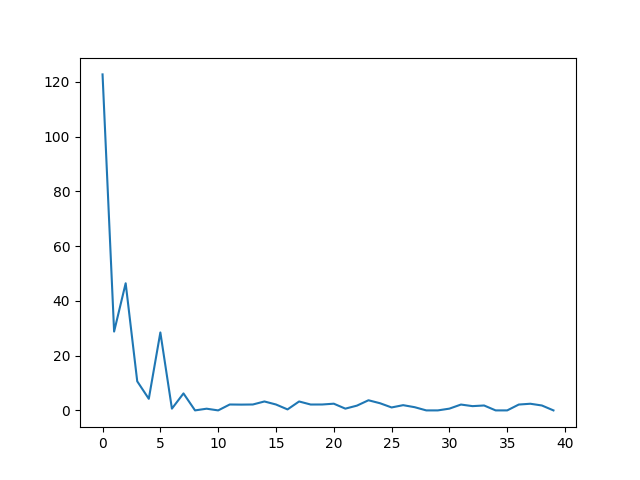
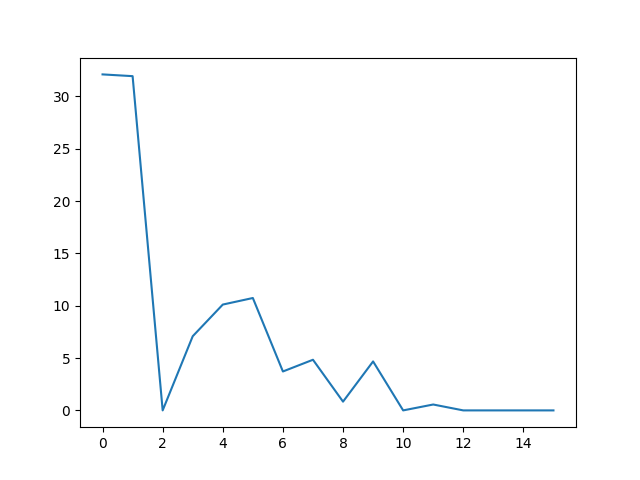
下面给出在 \(10 \times 10\) 网格下实验的结果: 使用 SGD 优化 使用策略提升定理优化
注意到数值优化算法都受到了非凸优化的限制,在最小值周围波动。但是梯度和非梯度的优化原理不同,可以互补,我们可以把两者方法结合使用,先使用非数值优化,在最小值附近再采用用梯度优化:结合方法优化
另一方面,在实践中注意到虽然基于策略提升定理的迭代轮数很少,但是由于矩阵求逆的高复杂度,所需时间难以接受。
但是,综合之前的分析,我们知道迭代法和求逆法是相近的方法。我们可以使用有限的 \(q_n\) 来代替 \(q^\pi\) 。上述代码中也实现了替代方法,用 \(q_5\) 作为 \(q\) 的近似。
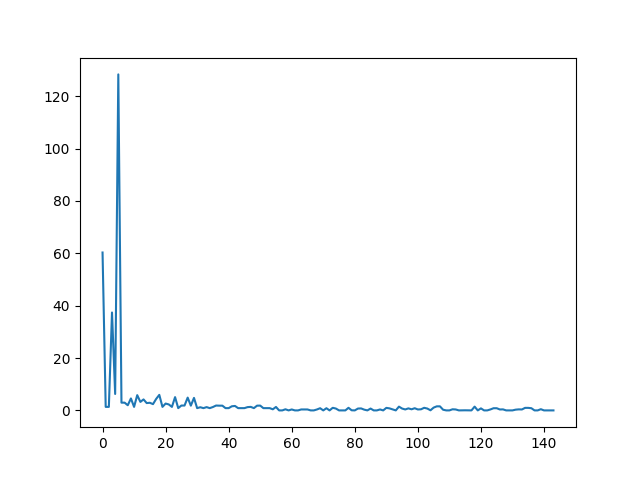
为了凸显时间差距,让网格变大为 \(20\times 20\) ,虽然近似法收敛所需轮数更多,但是时间却远短于求逆,仅用 6 秒就完成了求逆法 12 秒的计算。对比结果如下:求逆法 近似法
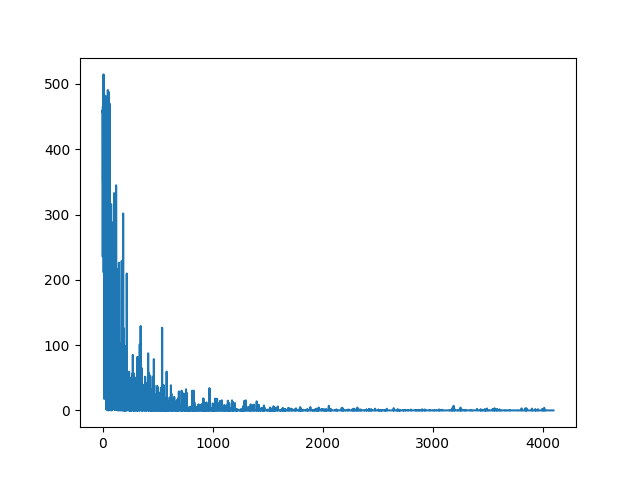
当网格大小变为 \(30\times 30\) ,近似法的优势完全体现。此时求逆法计算时间大于30秒,但是近似法在 16 秒就收敛,和 Q-Learning 所用的 14 秒不相上下,并取得了更优的收敛效果。近似法 Q-Learning
总结 使用线性代数的方法,摆脱了基于泛函分析的收敛性证明,让算法更加明了。上文提到的迭代法和近似法可证明等价为策略提升和价值提升;不过由本文导出的新无约束优化思路,虽然在确定性问题上难与传统方法竞争,却可以在高维空间中与降维等方法充分配合,达到类似 DQN 的效果。