正态分布是一个二次型
\[ f(\mathbf{x}) = \frac{1}{(2\pi)^{n/2}|\Sigma|}\exp\left( -\frac{(\mathbf{x - \mu})^\text{T}\Sigma^{-1}(\mathbf{x - \mu})}{2} \right) \]
这是多元正态分布的概率密度函数。其中,\(\mathbf{x} = (x_{1},x_{2},\dots,x_{n})^\text{T}\) 是正态分布的取值, \(\mathbf{\mu} = (\mu_{1},\mu_{2},\dots,\mu_{n})^\text{T}\) 是均值向量,而 \(\Sigma\) 是该分布的协方差矩阵。
一个特别的情况是各分量独立。此时,\(\Sigma\) 是一个对角阵。从正态分布中独立同分布地采样也是这种情况。
为了方便分析,从下面开始,我们把所有的随机变量进行中心化:对于随机变量 \(X\),定义 \(Z = X - \mu\),则 \(Z\) 的期望为 0。则概率密度简化如下:
\[ f(\mathbf{z}) = \frac{1}{(2\pi)^{n/2}|\Sigma|}\exp\left( -\frac{\mathbf{z}^\text{T}\Sigma^{-1} \mathbf{z}}{2} \right) \]
我们不难看出,对于归一化之后的多元正态随机变量,其性质被协方差矩阵 \(\Sigma\) 完全决定。
这个完全决定贡献了这么一条性质:
- 如果两个服从正态分布的随机变量不相关,那么他们独立。
这并不难理解:如果这两个变量不相关,则协方差矩阵是对角阵。这和独立的情况是一样的。既然不相关和独立有相同的协方差矩阵,而正态分布由协方差矩阵完全决定,则不相关就是独立。
而协方差矩阵是一个非负实对称矩阵,和我们比较熟悉的二次型比较相似。准确来说,对应的二次型总是圆(超球)或椭圆(超椭球)。事实上,圆和椭圆正是正态分布密度函数的等值线图:
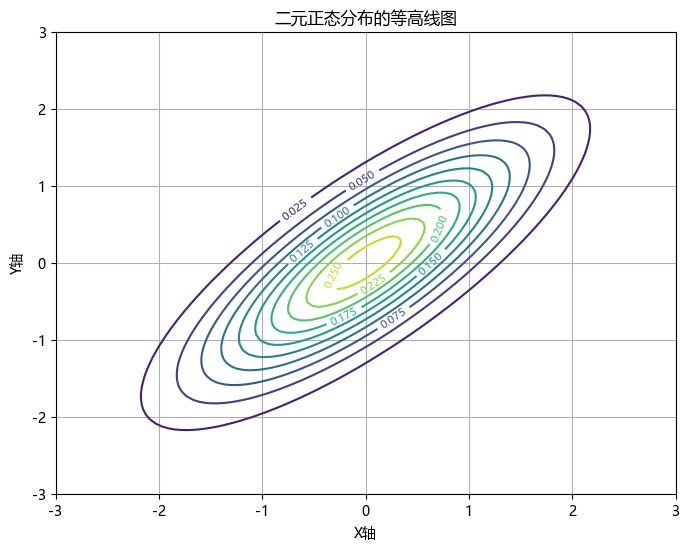
上图是 \(\Sigma = \begin{bmatrix}1&0.8\\0.8&1\end{bmatrix}\) 的等值线图。
既然已经知道 \(\Sigma\) 是一个非负实对称矩阵,一个自然的想法是对它做特征值分解:
\[ \begin{aligned} \Sigma &= P\Lambda P^{\text{T}} \\ \Sigma^{-1} &= P^\text{T}\Lambda^{-1}P \end{aligned} \]
从线性代数我们知道,\(P\) 必然可以取为一个规范正交阵(\(PP^\text{T} = I\))。
带入表达式:
\[ f(\mathbf{z}) = \frac{1}{(2\pi)^{n/2}|\Lambda|}\exp\left( -\frac{(P\mathbf{z})^\text{T}\Lambda^{-1}P\mathbf{z}}{2} \right) \]
我特地写成了 \((P\mathbf{z})^\text{T}\Lambda^{-1}(P\mathbf{z})\),是因为这样的事实:
- 如果 \(\mathbf z\) 遵循协方差为 \(\Sigma = P\Lambda P^\text{T}\) 的多元正态分布,则 \(P\mathbf{z}\) 遵循协方差为 \(\Lambda\) 的多元正态分布。考虑到 \(\Lambda\) 是一个对角阵,也就是说,\(P\mathbf{z}\) 的各分量独立。
这个证明很简单。因为 \(P\mathbf{z}\) 关于 \(\mathbf z\) 的雅可比矩阵就是 \(P\),而 \(P\) 作为规范正交阵,行列式绝对值为 \(1\),所以:
\[ f(P\mathbf{z}) = |P|f(\mathbf{z}) = f(\mathbf{z}) = \frac{1}{(2\pi)^{n/2}|\Lambda|}\exp\left( -\frac{(P\mathbf{z})^\text{T}\Lambda^{-1}P\mathbf{z}}{2} \right) \]
考虑这个结论的几何意义:规范正交阵 \(P\) 的作用效果其实是对向量进行旋转。
以上面的图为例:原来的 \(X\) 与 \(Y\) 并不独立,是因为椭圆的短轴和长轴并不在坐标轴上,而是在他们之间。对协方差矩阵做特征值分解:
\[ \Sigma = \begin{bmatrix} 1 & 0.8 \\ 0.8 & 1 \end{bmatrix} = \frac{1}{\sqrt{ 2 }}\begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} 1.8 & 0 \\ 0 & 0.2 \end{bmatrix} \frac{1}{\sqrt{ 2 }}\begin{bmatrix} 1 & 1 \\ -1 & 1 \end{bmatrix} \]
按照特征值分解结果,如果定义新的随机变量 \(Z_{1} = \frac{1}{\sqrt{ 2 }}(X+Y),Z_{2} = \frac{1}{\sqrt{ 2 }}(X - Y)\),则 \(Z_{1}\) 与 \(Z_{2}\) 相互独立,方差分别为 1.8 和 0.2。
从图像上也能看出这个结果:椭圆的长轴方向向量是 \((1,1)^\text{T}\),短轴则是 \((1,-1)^\text{T}\),所以如果把坐标轴旋转到这两个方向,新的椭圆就是正的,对应独立的情况。
如果我们沿着这条路继续走下去,就可以得到主成分分析在正态分布的特殊情况:
- 我们对协方差矩阵特征值分解,将得到的变换 \(P\) 作用在 \(\mathbf z\) 上,得到的新随机向量各个分量独立(协方差为 0)。
把所有的“协方差”换成“样本协方差”:
- 我们对样本协方差矩阵特征值分解,将得到的变换 \(P\) 作用在 \(\mathbf z\) 上,得到的新随机向量各个分量样本协方差为 0,按照最大似然估计原则,原协方差也最有可能是 0。
总的来说,要理解这些点:
- 中心化之后的正态分布被一个二次型矩阵(协方差矩阵)决定
- 可以对正态分布进行线性变换(可逆矩阵乘),得到的结果仍然是正态分布
- 有相关性的正态分布可以通过旋转变换变成不相关的正态分布(主成分分析)
- 因为正态分布被协方差矩阵决定,所以不相关就是独立
- 从上一点可以得出,如果协方差矩阵是一个分块对角阵:
- \(\Sigma = \begin{bmatrix}\Sigma_{k} & O\\O & \Sigma_NaN\end{bmatrix}\)
- 那么前 \(k\) 个分量构成的随机向量 \(Z_{k}\) 和后 \(n-k\) 个分量构成的随机向量 \(Z_{n-k}\) 是独立的,进一步,由前 \(k\) 个分量的函数结果与后 \(n-k\) 个分量的函数结果也是独立的。