傅里叶级数的可视化实践
在之前对傅里叶级数的介绍中,我提到,复值函数的傅里叶级数实际是把复平面上的一段曲线转换为可数个旋转速度、半径不同的圆周运动的组合。这次,我们就用代码来做一次可视化。
使用的库是 3b1b 视频中采用的 manim 库的社区维护版。链接在此。
代码
SVG 处理
manim 库提供了 SVGMobject 类型,专门处理 SVG 图像。
我们使用 .family_members_with_points() 取出图像各个独立的部分,然后根据需要的视觉效果进行居中和放缩,返回指定的图像部分。1
2
3
4
5
6
7
8def getPath(self, filePath, index=0) :
path = SVGMobject(filePath).family_members_with_points()[index]
path.set_fill(opacity=0).set_stroke(WHITE, 0)
path.scale(min(
7 / (path.get_right() - path.get_left())[0],
4 / (path.get_top() - path.get_bottom())[1]
))
return path
级数计算
对于 SVGMobject,可以用 .point_from_proportion(alpha) 按比例取点。其中 \(\alpha \in [0,1]\),相当于我们有 \(f(t),t \in [0,1]\) 表示复平面上的图像。
我们用 \(\sum_{k=0}^{N} f(k\Delta t) e^{-\mathrm i2n\pi k \Delta t}\Delta t\) 代替 \(\int_0^1 f(t)e^{-\mathrm i2n\pi t}\mathrm dt\) 来计算各级数的系数。
实现上来说,对于不同的 \(n\),\(f\) 是不变的,可以把 \(\left\{f(k\Delta t)\right\}\) 采样为一个 ndarray,对于每个 \(n\) 再把 \(\left\{e^{-\mathrm i2n\pi k \Delta t}\Delta t \right\}\) 生成为一个 ndarray,最后再把两个 ndarray 做点乘实现积分,用 numpy 降低计算的复杂度。
更进一步,我们可以把所有的 \(n\) 对于的向量合并为一个矩阵,用一次矩阵乘法得到所有系数:1
2
3
4
5
6
7
8
9
10
11
12def calcParams(self, path: SVGMobject, samples_n = 1e3, freqs_n = 1000) :
dt = 1 / samples_n
ts = np.arange(0, 1, dt)
points = np.array([path.point_from_proportion(t) for t in ts])
points = points[:, 0] + 1j * points[:, 1]
self.freqs_n = freqs_n
self.freqs = 2 * np.array([self.id(i) for i in range(freqs_n)]) * PI * 1j
es = np.exp(np.matmul(ts.reshape(-1, 1), -self.freqs.reshape(1, -1))) * dt
self.params = np.squeeze(np.matmul(points.reshape(1, -1), es))
self.id 是一个编号函数,它把自然数下标按照 \(0,-1,1,-2,2,...\) 的顺序对应到频率 \(n\):1
2def id(self, n) :
return (n + 1) // 2 * (-1 if n % 2 else 1)
逐帧渲染
对于每一个圆的半径,我们在创建时就可以根据 self.params 确定其半径、旋转速度和初始位置,计算如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30def createVector(self, start, end, n) :
vec = Line([start.real, start.imag, 0], [end.real, end.imag, 0])
vec.set_stroke(
color=WHITE,
# sigmoid opacity 突出主要级数
opacity=1/(1+exp(-vec.get_length()))
)
# 计时器、频率
vec.tim, vec.n = 0, n
vec.add_updater(self.updater)
return vec
def drawer(self) :
# 计算级数以及级数和
self.series = self.params
self.sum = np.cumsum(self.series)
self.lastCalcTime = 0
drawer = VGroup()
for i in range(self.freqs_n) :
# 起点为前面的级数和,终点为加上自己的级数和
c, z = self.series[i], self.sum[i]
vec = self.createVector(z - c, z, i)
drawer.add(vec)
if i == self.freqs_n - 1 :
pen = TracedPath(vec.get_end)
drawer.add(pen)
self.add(drawer)
注意到代码使用 VGroup 统一管理线段,同时为最后一个线段添加了画笔,追踪其终点位置。
上一段代码中调用的 updater 函数在每一帧被调用,用来更新线段的位置。updater 可以有两个参数:需要更新的线段以及离上一次调用 updater 过去的时间。显然,对于每一帧,我们只需要计算一遍级数即可。所以,我用了一个不太优雅的方法:记录上一次计算级数的时间。如果到了新的一帧,就更新级数和时间,保证级数只算一次。
计算级数的过程和之前的积分基本相同,都是向量化加速运算。1
2
3
4
5
6
7
8
9
10
11
12
13def updateSeries(self, n, t) :
if self.lastCalcTime < t :
self.lastCalcTime = t
self.series = self.params * np.exp(self.freqs * t)
self.sum = np.cumsum(self.series)
def updater(self, vec: Line, dt) :
vec.tim += dt / 4
self.updateSeries(vec.n, vec.tim)
c, z = self.series[vec.n], self.sum[vec.n]
# 确定新的方向和位置
vec.set_angle(phase(c))
vec.shift([z.real, z.imag, 0] - vec.get_end())
生成视频
一个补充的细节是使用 \(\LaTeX\) 显示级数的前几项:1
2
3
4
5
6
7
8
9
10
11
12
13def tex(self, expand_n = 5) :
expand_n = min(expand_n, self.freqs_n)
texcontent = NAME + "$(t) ="
for i in range(expand_n):
z = self.params[i]
texcontent += "(%.2f+%.2fi)e^{%d\\pi i t} + " % (z.real, z.imag, 2 * self.id(i))
texcontent += "...$"
tex = Tex(texcontent)
tex.scale(12 / (tex.get_right() - tex.get_left())[0])
tex.to_edge(UP)
self.add(tex)
最后在 Scene 基类的 construct 方法中调用 tex 与 drawer 即可。
完整代码如下:
1 | from manim import * |
实践
一个有趣的发现是,Arrow 的渲染速度比 Line 要慢约三分之一。
为了展示不同数量的级数对于结果的影响,我将一个 \(\pi\) 的轮廓从 8 项至 1024 项进行了展开,对比结果如下:







感觉 64 那组还怪可爱的
理论上 1024 项不会有人眼可识别的误差。但是受到帧率限制,总有地方无法走出锐角拐弯。
另外附上其他的一些结果: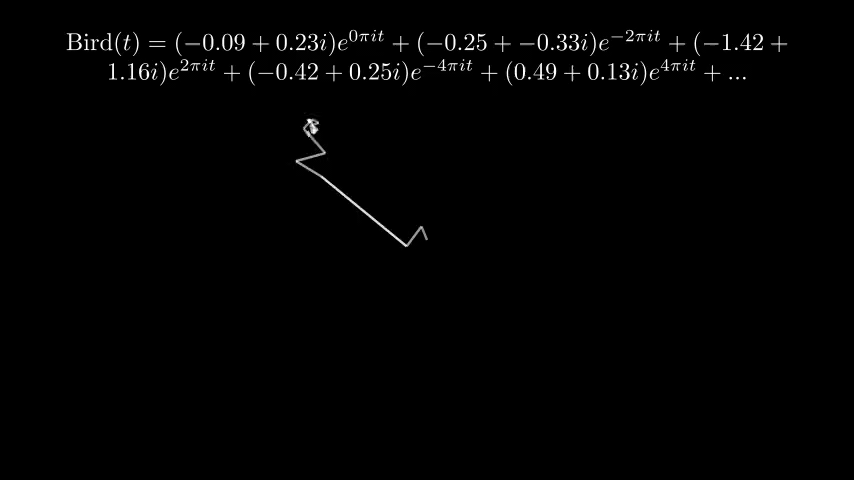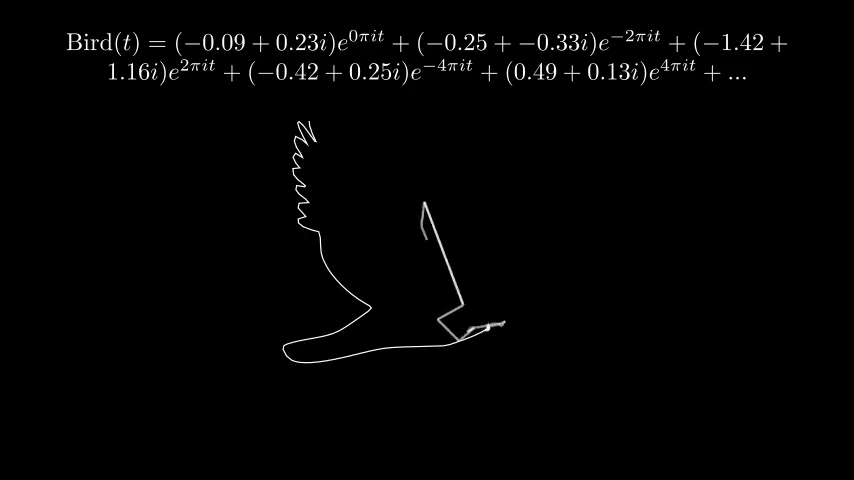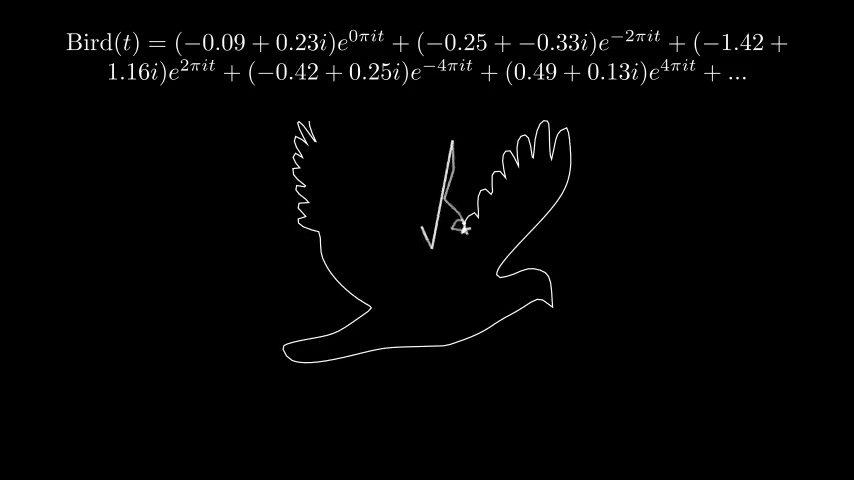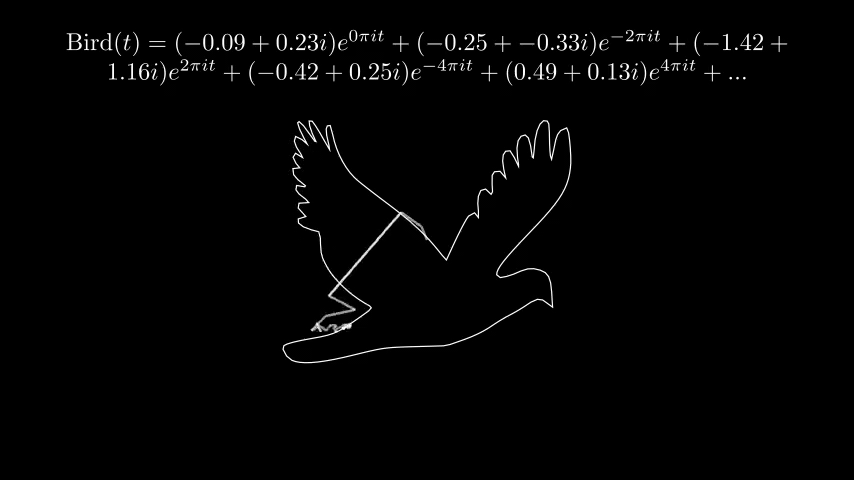
鸽子才不是在说我鸽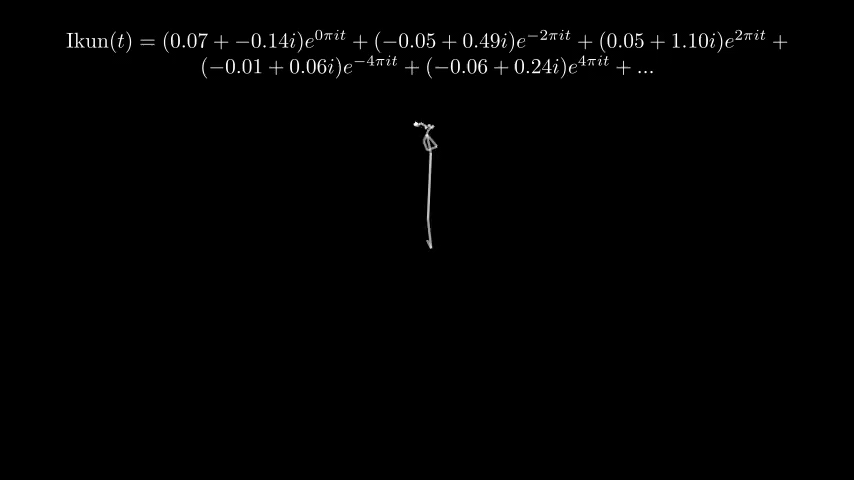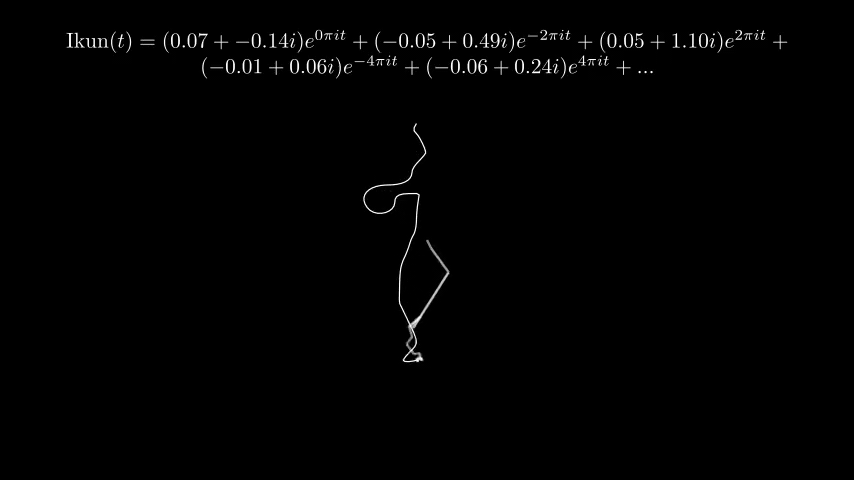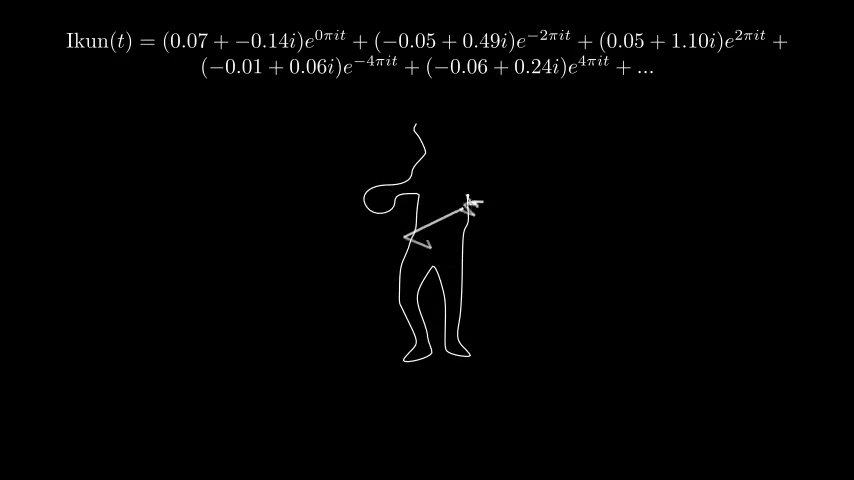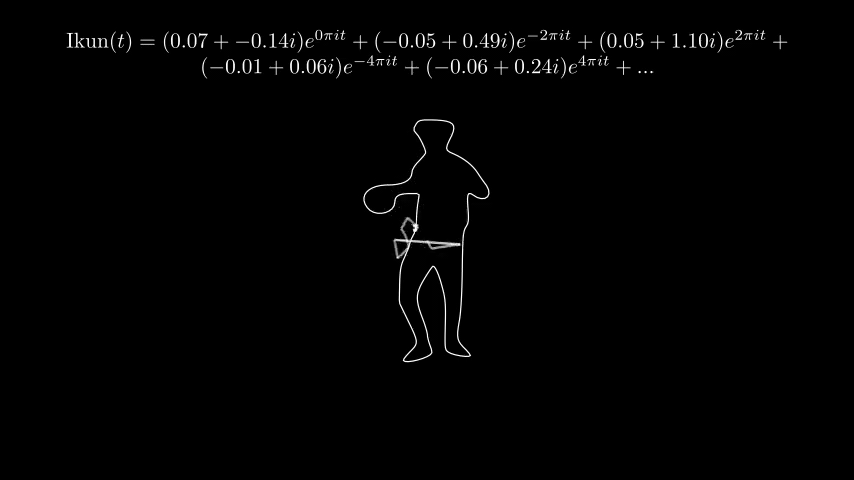
科学史学家联合考古队员今天证实,法国著名数学家、物理学家傅里叶或是一名小黑子。根据他关于傅里叶级数的手稿,我们复原出了上面的珍贵图像。