概率小题2
概要
- 随机变量
- 期望与方差
- 二项随机变量
- 泊松随机变量
随机变量
随机变量是在支撑集 \(S\) 上定义的以一定概率取到 \(S\) 中的元素的一个函数。
对于所有取实值的随机变量 \(X\),我们都可以定义一个函数 \(F(x)= P\{X \le x\}\),这被称为 累积分布函数(cumulative distribution function) 或者 分布函数(distribution function)。
离散随机变量
定义在大小可数的支撑集 \(S\) 上的随机变量称为离散随机变量。比如,在掷骰子的试验中,骰子上面的点数就是一个离散随机变量,因为 \(S=\{1,2,3,4,5,6\}\),大小可数。
我们定义离散随机变量 \(X\) 的概率质量函数(probability mass function) \(p(a)\) 如下:
\[ p(a) = P\{X = a\} \]
显然,根据概率的定义,有:
\[ \begin{aligned} 0 \ge p(a) \ge 1 \\ \sum_{a \in S}{p(a)}=1 \end{aligned} \]
例题 2a
对于定义在 \(N\) 上的随机变量 \(X\),假设它的质量函数是 \(p(i)=\frac{c \lambda ^i}{i!}\),其中 \(c\) 是一个未确定的常数,而 \(\lambda\) 是一个参数,求 \(c\) 的值。
由上面提到的质量函数的性质易得:
\[ \begin{aligned} c\sum_{i=0}^{\infty}{\frac{\lambda^i}{i!}}&=1 \\ \Rightarrow c &= e^{-\lambda} \end{aligned} \]
其中,我们用到了 \(\exp\) 函数的级数形式:\(\exp(x)=\sum_{i=0}^{\infty}{\frac{x^i}{i!}}\)。
这个函数在之后还会遇到,它被称作泊松分布。
期望(Expected Value)
我们定义一个定义在 \(S\) 上,质量函数为 \(p(x)\) 的随机变量 \(X\) 的期望 \(E[X]\) 如下:
\[ E[X]=\sum_{x\in S}{xp(x)} \]
从形式上看,这是所有 \(S\) 中的元素根据他们的概率所做的加权平均数。另一个理解是当 \(X\) 重复取无穷多次时我们得到的 \(X\) 的平均值(严格证明这一点的是中心极限定理,我们将在很后面谈到)。
比如掷骰子的期望:
\[ E[X]=\sum_{i=1}^{6}ip(i)=1(\frac{1}{6})+2(\frac{1}{6})+3(\frac{1}{6})+4(\frac{1}{6})+5(\frac{1}{6})+6(\frac{1}{6})=3.5 \]
注意到,掷一次骰子绝不可能得到 $ 3.5 $ 点,但是当我们反复重复,我们可以 期望 得到的平均点数是 $ 3.5 $。这大概是期望名字的来历。
随机变量的函数仍是随机变量
这是显然的命题。如果函数 \(g\) 的定义域是支撑集 \(S\),而值域是 \(U\),则 \(g(X)\) 就是一个定义在 \(U\) 上的随机变量。
既然这样,\(g(X)\) 就可以有自己的概率质量函数,也就可以有自己的期望。
例题 4a
比如 \(g(x)=x^2,P\{X=-1\}=0.2,P\{X=1\}=0.3,P\{X=0\}=0.5\),我们可以计算 \(E[g(X)]\):
不妨让 \(Y=g(X)\)。我们来看看 \(Y\) 的支撑集,应该是 \(\{0, 1\}\),而概率要由 \(X\) 的概率得到:
\[ P\{Y=1\}=P\{X=1\}+P\{X=-1\}=0.5,P\{Y=0\}=P\{X=0\}=0.5 \]
这样,根据定义,\(E[Y]=0(0.5)+1(0.5)=0.25\)。
随机变量函数的期望
我们不能每次都像 4a 里一样计算随机变量函数的期望。最好有一个通用的公式。
\[ \begin{aligned} E[g(X)]&=\sum_{a \in U}{ap_g(a)} \\ &=\sum_{a \in U}{\sum_{g(x)=a}g(x)p(x)} \\ &= \sum_{x \in S}g(x)p(x) \end{aligned} \]
期望的线性性
在上面的公式带入 \(g(x)=kx+b\),我们立刻得到:
\[ \begin{aligned} E[kX+b]&=\sum{(kx+b)p(x)}\\ &=k\sum{xp(x)}+b\sum{p(x)}\\ &=kE[X]+b \end{aligned} \]
也即期望具有线性性。
这不仅体现在线性变换。如果有两个定义在同一支撑集上的独立随机变量 \(X,Y\),我们也有
\[ \begin{aligned} E[X+Y]&=\sum_{x}\sum_{y}{(x+y)p_x(x)p_y(y)}\\ &=\sum_x\sum_yxp_x(x)p_y(y)+\sum_y\sum_xyp_x(x)p_y(y)\\ &=\sum_x{xp_x(x)\sum_yp_y(y)} + \sum_y{yp_y(y)\sum_xp_x(x)}\\ &= \sum_x{xp_x(x)} + \sum_y{yp_y(y)}\\ &=E[X]+E[Y] \end{aligned} \]
而且,既然 \(X,Y\)是独立的,那么 \(E[XY]=\sum_x\sum_yxyp_x(x)p_y(y)=[\sum_xxp_x(x)][\sum_yyp_y(y)]=E[X]E[Y]\)。这也是很重要的。
方差(Variance)
除了平均情况之外,另一个让人好奇的就是数据的离散程度,或者说,数据距离期望有多远。
一个简单的想法就是做差。但是,做差可能是一正一负,导致看上去相隔很远的数据差距抵消。所以我们需要一个非负的函数,可以是绝对值或者偶数次方。最终我们选择了相对简单又有良好数学性质的平方。(绝对值也可以是一种衡量,但是它并不处处可导,而且无法像平方一样放大极端数据的影响)
具体来说,我们定义一个随机变量的 方差 如下:
\[ Var(X)=E[(X-E[X])^2] \]
还算形象,它描述了随机变量的可能取值与期望之间的平均差距。
还是以骰子为例,掷骰子的方差是:
\[ (1-3.5)^2(\frac{1}{6})+(2-3.5)^2(\frac{1}{6})+...+(6-3.5)^2(\frac{1}{6})=\frac{35}{12} \]
另一种形式
利用之前说的期望的性质,我们不妨将方差展开:
\[ \begin{aligned} Var(X)&=E[(X-E[X])^2] \\ &= E[X^2-2E[X]X+(E[X])^2] \\ &= (E[X])^2+E[X^2]-2E[X]E[X] \\ &= E[X^2]-(E[X])^2 \end{aligned} \]
这是方差最常用的计算式。它更加简单,还是以骰子为例,只要算 \(\frac{(1^2+2^2+...+6^2)}{6}-3.5^2\) 即可。
方差的非负性
由定义就可以看出,方差是 \((X-E[X])^2\) 的平均值。既然这个平方项是非负的,那么它的均值也一定是非负的。
从另一方面,这意味着 \(E[X^2] \ge (E[X])^2\)。这其实是 Jensen 不等式的一个简单形式,注意到 \(f(x)=x^2\) 是凸函数,所以有 \(E[f(X)] \ge f(E[X])\)。证明可以看这里。
这个不等式很重要,我们将很快用到。
例题 5b(朋友悖论)
在这个问题中,我们认为朋友关系是一种有自反性(我是我朋友的朋友),不具有传递性(朋友的朋友不一定是我的朋友)的二元关系。显然我们可以把人际关系抽象为一个无向图 \((V,E)\)。在 \(V\) 上定义两个随机变量 \(X,Y\),\(X\) 的值在所有点中等可能选取(相当于自己),而 \(Y\) 的值在所有边的端点中等可能选取(相当于朋友)。
我们用 \(C(x)\) 表示 \(x\) 的朋友个数,证明:对于任何一组人际关系,有 \(E[C(X)] \le E[C(Y)]\)。也就是说,平均上来说,一个人总是比他的朋友有更少的朋友。
证明:
\[ \begin{aligned} E[C(Y)]&= \sum_y{C(y)\frac{1}{2|E|}}\\ &= \sum_{x \in V}{C(x)\frac{C(x)}{2|E|}} \\ &= \frac{\sum_{x}{C^2(x)}}{2|E|} \\ \end{aligned} \]
上面的第二个等号其实是在对每个点统计贡献,看它是多少条边的端点。注意到 $ 2|E|=_x{C(x)}$,则有:
\[ \begin{aligned} E[C(Y)] &= \frac{\sum_{x}{C^2(x)}}{\sum_x{C(x)}} \\ &= \frac{\sum_{x}{\frac{C^2(x)}{|V|}}}{\sum_x\frac{C(x)}{|V|}} \\ &= \frac{E[C^2(X)]}{E[C(X)]} \end{aligned} \]
既然 \(E[X^2]\ge (E[X])^2\),我们就有:
\[ E[C(Y)] \ge E[C(X)] \]
得证。
从直觉上思考一下原因:\(Y\) 的取值是在边的端点中随机选取,所以拥有朋友数量越多的的人越有可能成为 \(Y\)。
方差的(平方)线性性
由方差的计算公式和期望的线性性,我们可以得到:
\[ \begin{aligned} Var(kX+b)=&E[(kX+b)^2]-(E[kX+b])^2 \\ =&k^2E[X^2]+2kbE[X]+b^2\\ &-k^2(E[X])^2-2kbE[X]-b^2 \\ =&k^2Var(X) \end{aligned} \]
以及对于独立变量 \(X,Y\),我们有:
\[ \begin{aligned} Var(X+Y)=&E[(X+Y)^2]-(E[X+Y])^2 \\ =&E[X^2]+2E[XY]+E[Y^2]\\ &-(E[X])^2-2E[X]E[Y]-(E[Y])^2 \\ =&Var(X)+Var(Y) \end{aligned} \]
这里应用了独立变量 \(X,Y\) 的期望性质:\(E[XY]=E[X]E[Y]\)。
伯努利(Bernoulli)随机变量和二项(Binomial)随机变量
如果有一个定义在 \(\{0,1\}\) 上的随机变量 \(X\) 满足 \(P\{X=1\}=p,P\{X=0\}=1-p\)。 我们将这样的随机变量称为伯努利随机变量。
假设 \(X\)被重复取值了 \(n\) 次,一个让人感兴趣的量是 \(X=1\) 的次数。用 \(Y\) 来代表这个量,我们将 \(Y\) 称为二项随机变量。显然,伯努利随机变量有一个参数 \(p\),而二项随机变量还多了一个参数 \(n\)。
运用简单的组合知识,我们可以求出二项分布的概率质量函数:
\[ p(i)=P\{Y=i\}=C_n^ip^i(1-p)^{n-i},0 \le i \le n \]
运用二项式定理,我们知道这个概率质量函数是合理的,因为 \(\sum_{i=0}^np(i)=[p+(1-p)]^n=1\)。
以掷硬币为例,抛掷 \(n\) 次均匀的硬币就是一个 \(p=0.5\) 的二项分布。当 \(n=10\) 的时候,我们可以画出 \(p(i)\) 的图像: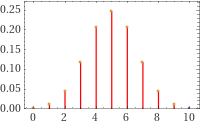
这符合直觉:5 次朝上的可能性最高,而全部朝上或朝下就不太可能。
二项分布的期望
如果 \(X\) 是一个参数为 \((n,p)\) 的二项随机变量,我们计算它的期望如下:
\[ \begin{aligned} E[X]&= \sum_{i=0}^n{iC_n^ip^i(1-p)^{n-i}}\\ &= \sum_{i=0}^{n-1}(i+1)C_n^{i+1}p^{i+1}(1-p)^{n-i-1}\\ &= \sum_{i=0}^{n-1}p(i+1)\frac{n}{i+1}C_{n-1}^ip^i(1-p)^{n-1-i} \\ &= np\sum_{i=0}^{n-1}C_{n-1}^ip^i(1-p)^{n-1-i} \\ &= np \end{aligned} \]
第三个等号利用了组合数的性质:\(C_{n+1}^{m+1}=\frac{n+1}{m+1}C_n^m\)。而第五个等号则利用了上面提到过的二项式定理。
这也符合直觉。如果我们抛 \(n\) 次硬币,最直接的期望就是它会朝上 \(\frac{n}{2}\) 次。
二项分布的方差
用和上面几乎一样的方式,我们有:
\[ \begin{aligned} E[X^2]&= \sum_{i=0}^n{i^2C_n^ip^i(1-p)^{n-i}}\\ &= \sum_{i=0}^{n-1}(i+1)^2C_n^{i+1}p^{i+1}(1-p)^{n-i-1}\\ &= \sum_{i=0}^{n-1}p(i+1)^2\frac{n}{i+1}C_{n-1}^ip^i(1-p)^{n-1-i} \\ &= np[\sum_{i=0}^{n-1}iC_{n-1}^ip^i(1-p)^{n-1-i} + \sum_{i=0}^{n-1}C_{n-1}^ip^i(1-p)^{n-1-i}] \\ &= np[(n-1)p+1] \end{aligned} \]
最后一个等号的前一项其实是一个参数为 \((n-1,p)\) 的二项分布的期望,直接使用之前的结论即可。
所以我们有 \(Var(X)=E[X^2]-(E[X])^2=np(1-p)\)。
另一种视角
这样简洁的结果让我们不由得多问:为什么?
其实二项随机变量就是 \(n\) 个独立的伯努利随机变量的和。我们已经在前文花费了大量篇幅描绘随机变量和差的期望与方差。不难发现,二项分布的期望应该是 \(n\) 倍的伯努利随机变量的期望,方差亦然。(\(X+X\) 和 $ 2X$ 并不是同一个是随机变量,前者的方差是两倍,后者是四倍,这里是前者)
而伯努利变量的期望和方差就很简单。如果 \(Y\) 是参数为 \(p\) 的伯努利随机变量,则:
\[ E[Y]=1(p)+0(1-p)=p,Var(Y)=(1-p)^2p+p^2(1-p)=p(1-p) \]
这样一来,
\[ E[X]=nE[Y]=np,Var(X)=nVar(Y)=np(1-p) \]
二项随机变量概率最大的取值
这也是一个吸引人注意的问题。在一些情况下答案很显然,比如抛硬币,应该是 \(\frac{n}{2}\) 次最有可能;如果这是一个分数,那么 \(\frac{n+1}{2}\) 与 \(\frac{n-1}{2}\) 等可能。但如果是一般的参数 \((n,p)\) 呢?
这其实就是求 \(p(i)\) 的极值。也许你一下会想到做差(类比求导),但是对于这种带组合数的东西,逐项做商是更好的选择:
\[ \frac{p(i+1)}{p(i)}=\frac{C_n^{i+1}p^{i+1}(1-p)^{n-i-1}}{C_n^ip^i(1-p)^{n-i}}=\frac{n-i}{i+1}\cdot\frac{p}{1-p} \]
既然这个比值是递减的,我们就要找让这个式子小于 1 的第一个 \(i\)。
则有:
\[ (n-i)p<(i+1)(1-p) \Rightarrow i > (n+1)p-1 \Rightarrow i = \lfloor(n+1)p\rfloor \]
(一个小细节,用小于号和小于等于号是等价的,如果有多个最大值,这里会取较大的那一个)
如何计算
斯特林近似(Stirling’s approximation)
组合数的一大问题就是阶乘计算很慢,但我们可以使用 \(k!\sim(\frac{k}{e})^k\sqrt{2k\pi}\),这样就能够用快速幂 \(\mathcal{O}(\log k)\) 计算。
这个近似的证明不在此给出,但有意思的是,当 \(k\) 变大的时候,绝对误差以指数速度变大,但是相对误差趋向于 0。
递推算法
其实在最大值中已经提到了。由于 \(p(i+1)=\frac{n-i}{i+1}\cdot\frac{p}{1-p}p(i)\),我们可以 \(\mathcal{O}(k)\) 全部递推。
例 6g
在美国的选举制度里,总统选举按照州来计票。一个州有一定的票数 \(a\),在州内进行投票,投出的相对多数候选人将会获得这个州的所有 \(a\) 张选票。你可以近似认为 \(a\) 与一个州的人口 $m $ 成正比。那么,在这种制度下,人口大州的一个选民是否比人口小州的一个选民拥有更大的 期望左右选票数?
我们只讨论两个候选人的情况:考虑一个人能够左右的选票数量 \(X\):
- 其他人投出了平局(或票差为 1),这个的人的抉择将会左右这个州的 \(a\) 张选票,即 \(X=a\)。
- 其他人以大于一的票差决定了相对多数,则 \(X=0\)。
考虑两种情况出现的概率。不妨假设所有州的所有人的投票都等概率投给其中一个候选人(事实复杂的多)。设 \(m=2n+1\),则第一种情况出现的概率是 \(C_{2n}^{n}(\frac{1}{2})^{2n}\)。那么一个人能够控制的期望选票数是 \(aC_{2n}^{n}(\frac{1}{2})^{2n}\)。考虑到
\[ a \sim n,C_{2n}^n=\frac{(2n)!}{n!n!}\approx \frac{(\frac{2n}{e})^{2n}\sqrt{4n\pi}}{(\frac{n}{e})^{2n}2n\pi}=\frac{2^{2n}}{\sqrt{n\pi}} \]
则 \(aC_{2n}^{n}(\frac{1}{2})^{2n} \approx \frac{a}{\sqrt{n\pi}} \sim \sqrt{n}\)。
所以当州人口数变大时,一个人的期望左右票数也会增大。(这是一个极为特殊的情况,因为两个候选人的概率正好是 $ $。如果这个概率改变为 \(p\),期望票数将会正比于 \((\frac{p(1-p)}{4})^n\sqrt{n}\),将不再是增函数)
省流:我们应该去人口大州投票。
泊松(Poisson)随机变量
还记得例题 2a 中提到的随机变量吗?它具有概率质量函数 \(p(i)=e^{-\lambda}\frac{\lambda^i}{i!},0!=1\)。我们将这样的随机变量称为泊松随机变量。显而易见的,它具有一个参数 \(\lambda\)。
下面是 \(\lambda = 5\) 时的图像: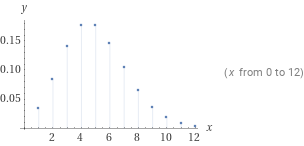
什么事件能用泊松随机变量精确描述
为了让我们能够正确理解泊松随机变量,在讨论它的数学性质之前理解实际意义是很重要的。
例题(来自数学桥)
小明是一个钓鱼爱好者。平均来说,他每小时可以钓上 \(\lambda\) 条鱼。问小明接下来一小时钓到 \(i\) 条鱼的概率是多少?
法一
考虑“每小时钓上两条鱼”的含义。相当于是,当 \(n\) 很大时,在 \(n\) 小时的时间中能钓上 \(\lambda n\) 条鱼。可以把这 \(\lambda n\) 条鱼看成均匀分布在时间轴上。一个小时钓 \(i\) 条鱼相当于在这段时间轴上取一个长度为 1 的区间,覆盖了正好 \(i\) 个点。我们可以把顺序反过来,先取一个区间,再把鱼随机分布。这样这就是一个二项分布。概率是 \(C_{\lambda n}^{i}(\frac{n-1}{n})^{\lambda n-i}(\frac{1}{n})^i\)。令 \(n \to \infty\),\(C_{\lambda n}^i \to \frac{\lambda ^i n^i}{i!}\),\((\frac{n-1}{n})^{\lambda n-i} \to e^{- \lambda}\),概率的极限就是 \(e^{-\lambda}\frac{\lambda ^i}{i!}\)。也就是泊松随机变量。
法二
考虑将一个小时划分为 \(n\) 段长为 \(\frac{1}{n}\) 的时间。当 \(n \to \infty\),在这段时间内,正好钓上一条鱼的概率可以记作 \(p_n\),则钓上大于一条鱼的概率一定是 \(o(p_n)\)(高阶无穷小)。(一瞬间不可能钓上来两条鱼)另外,\(p_n=\frac{\lambda}{n}+o(\frac{1}{n})\),这样才符合平均每小时 \(\lambda\) 条的假设。另一方面,不同的时间钓上鱼与否是独立的。所以,钓上 \(i\) 条鱼的概率就是 \(C_{n}^{i}(\frac{\lambda}{n})^{i}(1-\frac{\lambda}{n})^{n-i}\),极限也是 \(e^{- \lambda} \frac{\lambda^i}{i!}\)。
这两种方法其实都是不严谨的分析学过程,钓鱼也不一定有这么理想的条件,但理解意义即可。
泊松随机变量的期望
看到了上面的实际意义,就很容易猜测期望是 \(\lambda\)。事实上:
\[ \begin{aligned} E[X]&=\sum_{i=0}^{\infty}ie^{-\lambda}\frac{\lambda ^i}{i!} \\ &= e^{-\lambda}\sum_{i=0}^{\infty}\frac{\lambda ^{i+1}}{i!} \\ &= e^{-\lambda} \lambda e^{\lambda} \\ &= \lambda \end{aligned} \]
第二步使用了第一项是 0 的事实,并将 \(i+1 \to i\)。第三步则是 \(\exp\) 的级数展开式。
泊松随机变量的方差
这是泊松随机变量最有意思的一点:方差也是 \(\lambda\)。
\[ \begin{aligned} E[X^2]&=\sum_{i=0}^{\infty}{i^2e^{-\lambda}\frac{\lambda ^i}{i!}} \\ &= e^{-\lambda}\sum_{i=0}^{\infty}(i+1)\frac{\lambda ^{i+1}}{i!} \\ &= e^{-\lambda}\lambda (\sum_{i=0}^{\infty}i\frac{\lambda^i}{i!} + \sum_{i=0}^{\infty}\frac{\lambda ^i}{i!}) \\ &= e^{-\lambda}\lambda(\lambda e^{\lambda}+e^\lambda) \\ &= \lambda(\lambda + 1)\\ Var(X) &= E[X^2]-(E[X])^2 \\ &= \lambda \end{aligned} \]
其中第四步运用了之前得到的关于期望的表达式。
用泊松随机变量近似二项随机变量
在实际意义那里,我们已经发现,二项随机变量的极限就是泊松随机变量。事实上,这个极限收敛的并不慢。我们可以用泊松随机变量来近似一个二项随机变量:
\[ \begin{aligned} C_n^kp^k(1-p)^{n-k} &= \frac{n!p^k(1-p)^{n-k}}{(n-k)!k!}\\ &\approx \frac{n^k}{k!}(\frac{np}{n})^k(1-\frac{np}{n})^{n-k}\\ &\approx \frac{e^{-np}(np)^k}{k!} \end{aligned} \]
这是一个 \(\lambda=np\) 的泊松随机变量。
让我们看一看两个约等于需要什么条件:第一个要求 \(\frac{n^k(n-k)!}{n!} \approx 1\)。这不难,只要 \(n\) 略大,\(k\) 不太大就好。第二个要求 \(np\) 近似是一个常数。什么意思呢?\(p\) 应该是随着 \(n\) 会变化的,使得 \(np_n\) 是一个比 \(n\) 低阶的无穷大。
泊松概型(Poisson Paradigm)
这相当于能否使用泊松随机变量来描述问题的一个判别准则:
- 有 \(n\) 个事件,每个事件的发生概率是 \(p_i\),并且这些事件独立或弱相关
- 每一个事件的概率都很小
则事件发生的总数量就可以被看成一个 \(\lambda=\sum p_i\) 的泊松随机变量。