计算机绘图——复变函数和曼德勃罗集
本来,这只是一节普普通通的信息技术,直到阿梁同学跟我说:“我们来画一点有意思的吧!”
于是就有了:
复变函数
用亮度表示模长,用颜色表示辐角:
- \(f(z) = exp(z)\)

- \(f(z) = (2z - 1)^2(2z+1)\)

- \(f(z)=\sin(z)\)

曼德勃罗集
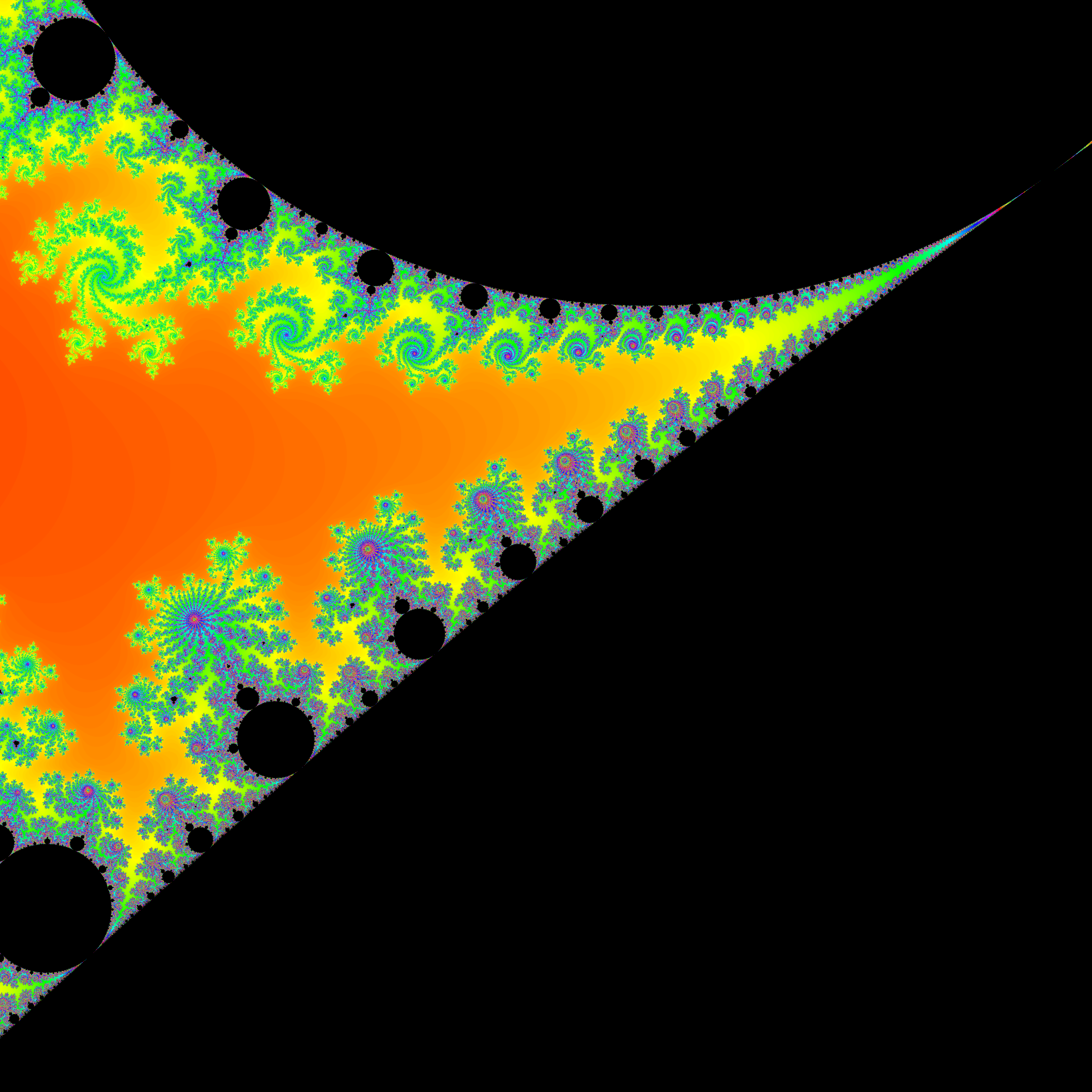
简介:对于函数 \(f(z)=z^2+c\),初始 \(z=0\)。我们反复地让 \(f(z) \to z\),如果 \(z\) 最终会收敛,就在 \(z\) 对应的复平面位置标上黑色;否则在 \(z\) 的位置按照发散速度标不同颜色。
有意思的是,这是一个分形。也就是说,边界的每一处都是完整的一个图形。无限细致。有“上帝的指纹”之称。
清晰度 4096x4096。




对曼德勃罗集的修改
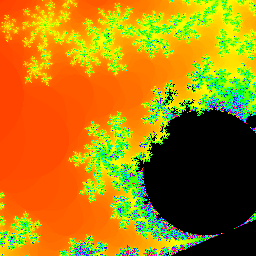
根据不同的函数,我们可以按照一样的方式画出图形。(我感觉还是曼德勃罗集好看)
清晰度 256x256。
- \(f(z)=z^2+z+c\)





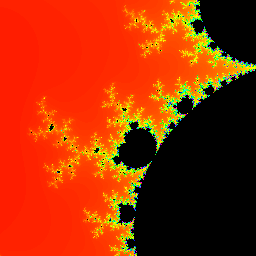
- \(f(z)=z^3+c\)



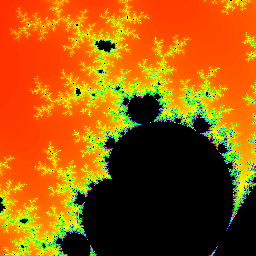
最后贴一贴代码吧
(其实最终渲染换了 C++,python 还是有点慢)1
2
3
4
5
6
7
8
9
10
11
12
13
14from PIL import Image
N = 256
def gen(foo) :
global N
im = Image.new(mode='HSV', size=(N, N))
w, h = im.size[0], im.size[1]
pix = im.load()
for i in range(w) :
for j in range(h) :
pix[i, j] = foo(i, j)
# print(pix[i, j])
return im1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58import cmath
import math
import time
scale = 1
cx, cy = 0, 0
def getc() :
cx, cy = 0, 0
ta = 0
for i in range(N) :
x = y = (i - N / 2) / N
x, y = foo3(x, y)
a = foo2(complex(x, y))
if a > ta :
cx, cy = x, y
ta = a
return cx, cy
def foo(x, y) :
global N, scale, cx, cy
tx, ty = (x - N / 2) / N, (y - N / 2) / N
# if ((tx - cx) ** 2 + (ty - cy) ** 2 < 0.01) :
# return (255, 0, 0)
tx, ty = foo3(tx, ty)
a = foo2(complex(tx, ty))
if a == 0 :
return (0, 0, 0)
return a % 256, 255, 255
# z**2+c 发散次数
def foo2(c) :
z = 0
global scale
for i in range(10000) :
z = z ** 2 + c
if abs(z) > 2 :
return (i + 1)
return 0
def foo3(x, y) :
global scale, cx, cy
return x / scale + cx, y / scale + cy
getc()
print(cx, cy)
for i in range(-2, 20) :
scale = 2 ** i
cx, cy = getc()
im = gen(foo)
im.show()
# im.convert('RGB').save(time.asctime(time.localtime(time.time())) + '.png')