概率小题
范围
贝叶斯公式,全概率公式。
简单推导连续情况下的贝叶斯公式:
回顾概率密度函数的定义:\(p(u)\) 是 \(P(x \le u)\) 的导数。所以我们能把 \(p(u)\) 写成一个极限的形式:\(p(u)=\lim_{u_1 \to u^-}\frac{P(u_1\le x\le u)}{u-u_1}\)。
这样,我们有:
\[ \begin{aligned} \frac{P_{x\mid y}(u_1\le x\le u \mid v_1\le y \le v)}{u-u_1} &= \frac{P_{y\mid x}(v_1\le y \le v \mid u_1\le x\le u)P_x(u_1\le x\le u)}{P_y(v_1\le y \le v)(u-u_1)} \\ &= \frac{\frac{P_{y\mid x}(v_1\le y \le v \mid u_1\le x\le u)}{v-v_1}P_x(u_1\le x\le u)}{\frac{P_y(v_1\le y \le v)}{v-v_1}(u-u_1)} \end{aligned} \]
令 \(u_1 \to u^-,v_1 \to v^-\),则有:
\[ p_{x\mid y}(u \mid v)=\frac{p_{y \mid x}(v \mid u)p_x(u)}{p_y(v)} \]
自己 YY 的题目
将一伯努利事件重复 \(2n\) 次,恰好得到 \(n\) 次正例和 \(n\) 次反例,求正例概率 \(q\) 满足 \(q \in [0.4, 0.6]\) 的概率是多少?
在试验开始之前,我们可以对 \(q\) 所遵从的概率分布做一个先验假设。假设 \(Pr(q \in [0, x])=\int_0^xp(q) \mathrm dq\),即 \(q\) 遵循概率密度函数为 \(p\) 的分布。一个合理的猜想是平均分布 \(p(q)=1\)。
为了方便,我们用 \(A\) 表示事件“恰好得到 \(n\) 次正例和 \(n\) 次反例”。
显然,\(A\) 是一个典型的二项分布。如果我们已知 \(q\),则可以知道 \(P(A|q)=C_{2n}^nq^n(1-q)^n\)。
则我们要求出的是 \(p(q \mid A)\)。使用针对连续型随机变量的贝叶斯公式以及全概率公式,我们得到:
\[ \begin{aligned} p(q \mid A) &= \frac{P(A \mid q)p(q)}{P(A)} \\ &= \frac{P(A\mid q)p(q)}{\int_0^1P(A \mid u)p(u)\mathrm du} \\ &= \frac{P(A \mid q)p(q)}{P(A)} \\ &= \frac{C_{2n}^nq^n(1-q)^np(q)}{\int_0^1C_{2n}^nu^n(1-u)^np(u)\mathrm du} \\ &= \frac{q^n(1-q)^np(q)}{\int_0^1u^n(1-u)^np(u)\mathrm du} \end{aligned} \]
运用 Beta 函数定积分,得到: \(p(q \mid A)= q^n(1-q)^np(q)\frac{(2n+1)!}{(n!)^2}\)。
如果假设先验分布是平均分布,则我们要求的结果为:
\[ \frac{(2n+1)!}{(n!)^2}\int_{0.4}^{0.6}q^n(1-q)^n\mathrm dq \]
这个东西没有闭合形式,但是我们可以快速验证完备性:当积分上下界是 0 和 1 时,结果是 1;当我们取 \(n=5\) 时,得到结果大约 \(0.506\),说明少量样本并不具有说服力;而当 \(n=100\) 时,结果接近为 1。
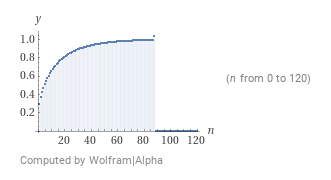
一个有趣的事实是,无论一开始的先验假设如何,只要没有一处函数值为 0,则最终我们的结果都会变成 1。这体现了实验是如何一步步改变我们的观点的。
读了一下才知道,自己随便提出的问题实际蕴含着贝叶斯定理的第一个应用:拉普拉斯接续准则(Laplace's rule of succession)。所以上面的就不再是自己 YY 的题目了,而是后面的例题 5e。
概率论基础教程
已经出现的公式:
\[ \begin{aligned} 0 \le P(E) &\le 1 \\ P(S)&=1\\ \forall i\ne j,E_i \cap E_j=\varnothing \Rightarrow P(\bigcup_{i=0}^{\infty}E_i) &= \sum_{i=0}^{\infty}{P(E_i)}\\ P(E\mid F)&=\frac{P(EF)}{P(F)}\\ P(E)&= \sum_iP(E\mid F_i)P(F_i)\\ P(F_j \mid E) &= \frac{P(E \mid F_j)P(F_j)}{\sum_i{P(E \mid F_i)}} \end{aligned} \]
例题 3o
这个例题告诉我们:不要相信自己的直觉。
在一个 \(10^6\) 个人的小镇里,过去十年共有 \(10^4\) 人犯罪(不养闲人)。发生了一起恶性案件,检察官认为,某一个有犯罪记录的人犯下这桩案件的概率是某一个没有犯罪记录的人犯下这桩案件的概率的 \(c\) 倍。现在,法医提供了新证据:在现场采集到了罪犯的 5 个关键 DNA 片段,正常人同时拥有这五个 DNA 片段的概率是 \(10^{-5}\)。警方掌握有犯罪记录的人的 DNA 库,立即进行了匹配,发现犯过罪的人中只有 A 匹配了 5 个片段。 如果检察官一开始的推测是正确的,那么在新证据下,A 是罪犯的概率是多少?
由题目可以获得先验概率:如果某个“良民”犯罪的概率是 \(b\),“惯犯”犯罪的概率是 \(a\),则有:\(10^4b+(10^6-10^4)a=1,a=cb\)。即 \(a=\frac{c}{10^4c+9.9\times10^4},b=\frac{1}{10^4c+9.9\times10^4}\)。
列出贝叶斯公式还是简单的。用 \(A\) 表示 A 是罪犯,\(B\) 表示有且只有 A 匹配 DNA,则:
\[ \begin{aligned} P(A \mid B) &= \frac{P(B\mid A)P(A)}{P(B)} \\ &= \frac{aP(B\mid A)}{P(B)} \end{aligned} \]
麻烦从这里开始。首先一个容易被直觉带偏的就是 \(P(B \mid A)\),看似是 1,但如果考虑 \(B\) 的定义,就会发现其实是 \((1-10^{-5})^{9999}\)。另一个更麻烦的就是 \(P(B)\)。很容易简单地看成 \(10^{-5}(1-10^{-5})^{9999}\)(这就是定义嘛)。问题在于,定义说的是“正常人”,但如果 A 是罪犯,那就不是 \(10^{-5}\) 而是 1。所以要继续根据 \(A\) 的真假来分讨。使用全概率公式:
\[ \begin{aligned} P(B) &= P(B \mid A) P(A) + P(B \mid A^c)P(A^c) \\ &= (1-10^{-5})^{9999}a + (1-a)P(B \mid A^c) \end{aligned} \]
别慌,如果你又把 \(P(B \mid A^c)\) 当成了 \((1-10^{-5})^{9999}\),说明你还是被直觉骗了。\(P(B \mid A)=(1-10^{-5})^{9999}\) 是因为如果 A 是罪犯那么别人都是“正常人”。但反之不然。如果 A 不是罪犯,其他“惯犯”也有可能是罪犯啊。所以一定不能轻信直觉。
设 \(C\) 表示“所有惯犯都不是罪犯”。现在定义可以使用了,\(P(B \mid C) = 10^{-5}(1-10^{-5})^{9999}\)。注意到 \(A^c \subset C\),并且 \(P(B \mid A^cC^c)=0\)(A 没犯罪但是惯犯犯罪,则必然有不是 A 的匹配,与 \(B\) 矛盾)则继续用全概率公式:
\[ \begin{aligned} P(B \mid A^c) &= P(B \mid A^cC) P(C \mid A^c) + P(B \mid A^cC^c)P(C^c \mid A^c) \\ &= P(B \mid C) \frac{P(CA^c)}{P(A^c)} + 0 \\ &= 10^{-5}(1-10^{-5})^{9999}\frac{1-10^4a}{1-a} \end{aligned} \]
综上,我们求的概率是 \(P(A \mid B)=\frac{a}{a+10^{-5}(1-10^4a)}=\frac{1}{0.9+\frac{10^{-5}}{a}}\)。
这个例子里的种种坑都是把某一个条件概率当成总概率使用导致的。所以要看清定义,并且多用一用全概率公式,不要想当然。
习题 3.21
这个习题告诉我们,有时不需要太过深入,而是要从整体上把握问题。
一个理想的公平硬币,A 扔了 \(n+1\) 次,B 扔了 \(n\) 次,求 A 正面次数大于 B 的概率。
设 \(P_n(>)\) 表示两人各扔 \(n\) 次 A 正面次数大于 B 的概率,\(P_n(\ge)\) 表示大于等于,以此类推。对 A 的最后一次分类讨论,我们发现答案是 \(\frac{1}{2}P_n(>)+\frac{1}{2}P_n(\ge)\)。这个东西看似难求,但是注意到 A 与 B 是对称的,所以 \(P_n(\ge)=P_n(\le)\),所以答案是 \(\frac{1}{2}(P_n(>)+P_n(\le))=\frac{1}{2}\)。
例题 4j
这个问题告诉我们,要善于转化。
历史上的一个真实问题:两个人在玩一种游戏,A 获胜的概率是 \(p\),约定 A 先赢 \(n\) 轮就算 A 赢,B 先赢 \(m\) 轮就算 B 赢。(比如 \(n=m=3\) 就是五局三胜)现在 A 已经赢了 \(a\) 局,B 赢了 \(b\) 局,求最终 A 获胜的概率。
有两种不同的分析方法。一种类似于概率 DP:用 \(f_{i, j}\) 表示 A 还差 \(i\) 局,B 还差 \(j\) 局时 A 赢的概率。容易得到:\(f_{i,0}=0,f_{0,j}=1,f_{i,j}=pf_{i-1,j}+(1-p)f_{i,j-1}\)。
这种方法的分析过程非常“tedious”,所以我们要考查另一种方法。
原问题的获胜条件可以等价转化如下:重复进行 \(n+m-1\) 轮,A 获胜了至少 \(m\) 轮。(五局三胜就是一个很好的例子)
所以在已经进行了 \(a+b\) 轮的情况下,A 要在剩下 \(N = n+m-a-b-1\) 轮中至少赢下 \(n-a\) 轮。运用二项分布的概率公式(这个超纲了):
\[ P=\sum_{i=n-a}^{N}{C_{N}^{i}p^i(1-p)^{N-i}} \]
例题 4k
技巧性不强,可以跳过。
考虑一场篮球比赛:当 A 队发球时,A 进球的概率是 \(p\);当 B 队发球时,A 进球的概率是 \(q\)。开局时 A 队发球。先进 \(n\) 个球的队伍获胜。请问 A 队的胜率是在连发规则(谁进球谁发)下高还是在换发规则(与谁进球无关,球权交替取得)下高?
为了方便,显然要使用上一题的技巧,让比赛进行 \(2n-1\) 轮。但是,由于每一队的发球数量未知,还是不好分析。既然 \(2n-1\) 轮中多出来的部分对于胜负没有影响,我们可以适当修改连发规则:当某一队达到 \(n\) 球时,接下来剩余的轮数全部由另一队发球。显然这不会影响胜负条件与概率。
换发情况下,A 队发球 \(n\) 次,B 队 \(n-1\) 次。而在连发情况下,未分出胜负时,当且仅当某一队进球之后才能拿到球权(第一个除外)。又由于被修改的规则,第 \(n\) 个进球之后也拿不到球权,所以胜利者正好会拿到 \(n-1\) 次球权,再加上开局 A 拿球权,也正好是 A 队发球 \(n\) 次,B 队 \(n-1\) 次。
注意到转换之后的规则已经跟进球顺序没有关系,那么既然两种规则发球次数相同,A 队的胜率也必然相同。
例题 4l
这个例题告诉我们:要相信自己的直觉。
已知有 \(r\) 个人,第 \(i\) 个人一开始有 \(n_i\) 个金币。每一轮,选出两个人进行公平的对决(石头剪刀布之类的),赢家从输家获得一个金币。如果某人没有金币了,那么就出局。最终的人(带着所有的 \(n\equiv \sum n_i\))就是赢家。求某个人是赢家的概率。
我们可以大胆猜测概率是 \(P_i=\frac{n_i}{n}\)。为什么呢?
我们可以对问题做一个转化:假设总共有 \(n\) 个人,每个人有一个金币。无论选择规则是什么,由于每个人地位均等,概率应该都是 \(\frac{1}{n}\)。接下来,我们把 \(n\) 个人分成 \(r\) 组,第 \(i\) 组有 \(n_i\) 个人。组内的竞争并不会对组的金币总数有影响,而组间的竞争相当于两个人的竞争。如果我们认定一个组获胜的条件是某个组员获胜,我们就发现组获胜的问题和原问题是等价的。而第 \(i\) 组获胜的概率是所有组员之和,即 \(P_i=\frac{n_i}{n}\)。
例题 4m
这个例题告诉我们,当直觉失败的时候,要记得使用 “tedious” 的方法。
在 4l 的基础上,令 \(r=2\),改变“公平对决”的获胜概率,让第 \(i\) 个人的胜率是 \(p_i\)(\(\sum_ip_i=1\)),求最终第 \(i\) 个人的胜率。
这个时候,没有什么转化是说得通的,但是 4j 中定义状态的方法仍然可以使用。我们定义 \(f_i\) 表示当第一个人有 \(i\) 个金币时他的胜率。则有:\(f_n=1,f_0=0,f_i=p_1f_{i+1}+p_2f_{i-1}\)。
这里有一个十分富有技巧性的转化:把 \(f\) 的三元关系转化成 \(f\) 的差分的二元关系。即 \(p_1(f_{i+1}-f_i)=p_2(f_i-f_{i-1})\) 或 \(f_{i+1}-f_i=\frac{p_2}{p_1}(f_i-f_{i-1})\)。
我们就可以将第二个公式累加,得到 \(f_i-f_1=f_1\sum_{j=1}^{i-1}{(\frac{p_2}{p_1})^j}\)。令 \(i=n\),则 \(1-f_1=f_1\sum_{i=1}^{n-1}{(\frac{p_2}{p_1})^i}\)。记 \(\frac{p_2}{p_1}=q\),对 \(q\) 分讨:
- \(q=1\),第一个人赢的概率就是 \(\frac{n_1}{n}\)。
- \(q\neq 1\),运用等比数列求和,\(f_1=\frac{1-q}{1-q^n}\),则 \(f_i=\frac{1-q^i}{1-q^n}\)。
例题 5e (Laplace's rule of succession)
这个例题告诉我们:太阳以高概率照常升起。
假设有 \(k+1\) 种硬币,第 \(i\) 种正面朝上的概率是 \(\frac{i-1}{k}\)。现在随机选择一个硬币,然后反复抛掷 \(n\) 次,已知这 \(n\) 次都是正面朝上,求第 \(n+1\) 次也是正面朝上的概率。
这个例题和开头 YY 的题有什么关系呢?硬币就是伯努利事件,而正例概率 \(q\) 恰恰就是在这里被随机选择。则拉普拉斯法则就是开头所说的问题的特化:我们要求全都是正例。我们所做的事情都是一样的,都是推测正例概率所遵从的概率分布。
当 \(k \to \infty\),就相当于我们在开头做出了先验假设:\(p(u)=1\)。
用事件 \(A_n\) 表示前 \(n\) 个都是正面。则 \(P(A_n \mid q=u) = u^n\),则 \(P(A_n)=\int_0^1{u^np(u)\mathrm du}=\frac{1}{n+1}\)。所以 \(P(A_{n+1} \mid A_n)=\frac{P(A_{n+1}A_n)}{P(A_n)}=\frac{n+1}{n+2}\)。
换句话说,如果你对一个事件一无所知,但是它已经发生了 \(n\) 次,我们可以假设正例概率遵循均匀分布,大胆预测下一次的概率是 \(\frac{n+1}{n+2}\)。
而依据我们开头的分析,我们完全可以进一步一般化这个准则:如果 \(n\) 次中正确了 \(m\) 次,我们可以猜测第 \(n+1\) 次的正例概率是 \(\frac{\int_0^1u^{m+1}(1-u)^{n-m}\mathrm du}{\int_0^1u^{m}(1-u)^{n-m}\mathrm du}=\frac{(m+1)!(n-m)!(n+1)!}{(n+2)!m!(n-m)!}=\frac{m+1}{n+2}\)。这也就是理论练习 3.30。
比如太阳已经连续升起了 \(365 \times 5\times 10^9\) 次,所以明天升起的概率是 \(\frac{365 \times 5\times 10^9+1}{365 \times 5\times 10^9+2}\)。