信息论基础-熵为什么是数据压缩的极限

由香农创立的信息论无疑是 20 世纪最伟大的成果之一——它直接影响了信息通信技术的发展。不过，信息论本身并不好懂。这篇文章想以一个尽可能简单的方式理解信息学的基础概念——信息熵，以及它的一些概念。

熵

定义

我们都听说过熵是数据压缩的极限，或者说一件事的信息量大小。但是不一定知道所以然。在下文中，我们将会明确证明这一点，但是我们要先给出信息熵的数学定义。

接下来的内容和熵的实际意义没有必然的关联，主要在解释数学表达式的一些性质。当然，将熵看作信息量的大小可以帮助我们理解。在这里提到这一点是想指出：这些性质是否成立与熵的实际意义无关，因此我们在后面证明熵的实际意义时没有循环论证的危险。

熵是一种关于随机变量的函数。如果一个离散随机变量 \(X\) 的可能取值集合是 \(\mathbb{X}\)，并且以 \(p\) 为概率分布（即 \(Pr(X=x)=p(x)\)）,那么定义 \(X\) 的熵 \(H(X)\) 为：

\[ H(X) = -\sum_{x \in \mathbb{X}}{p(x) \log p(x)} \]

（连续随机变量可以自然的扩展，但是性质会有所不同，本文就不涉及了）

其中当 \(\log\) 的底数是 2 时，单位为比特（bit），而底数为 \(e\) 时单位为奈特（nat）。

很容易发现 \(H(X)\) 是一个加权平均数或者说期望的形式，即 \(H(X)=-E_{p(x)}\log p(x)\)。

严格来说，熵是关于随机变量所遵从的分布的函数，它只与分布 \(p\) 有关，因此也被记作 \(H(p)\)。

对定义的解释

我们已经说过，时刻牢记熵的实际意义可以帮助我们推理。

如果熵真的表示数据压缩的极限，它的表达式就好像在说：我给 \(\mathbb{X}\) 中的每一个结果都赋予一个长度为 \(-\log p(x)\) 的编码，这样随机产生一个结果，我需要的平均编码长度就是 \(-E_{p(x)}\log p(x) = H(X)\)。

事实上正是如此，我们将在后面证明。现在我们来想另一个问题：如果我认为的概率分布是错的会怎么样？

比如 \(X\) 实际遵循 \(p(x)\) 的分布，但是我们认为的分布是 \(q(x)\)，所以我们自然会按照 \(-\log q(x)\) 的长度去编码。但是实际上每个结果的出现概率仍是 \(p(x)\)，则我们的平均编码长度就是 \(-\sum{p(x)\log q(x)}\)。

我们不妨将这个错误的长度记为 \(L_{wrong}(X)\)。它与 \(H(X)\) 哪个更好呢？

考虑做差：

\[ \begin{aligned} L_{wrong}(X) - H(X) &= \sum_{x \in \mathbb{X}}{p(x)(\log p(x) - \log q(x))} \\ &= \sum_{x \in \mathbb{X}}{p(x)\log \frac{p(x)}{q(x)}} \\ &= E_{p(x)}{\log \frac{p(x)}{q(x)}} \end{aligned} \]

这个差十分重要：它可以看作是衡量了 \(p(x)\) 与 \(q(x)\) 的差距，在机器学习中经常作为损失函数出现。我们将它单独拿出来，看一看它的性质。

相对熵

定义

刚才提到的 \(L_{wrong}(X) - H(X)\) 被称之为相对熵。你可以将它看成两种编码方式或者两种概率分布的差异，但是在没有证明实际意义之前，它还只是一个数学表达式。

定义关于两个概率分布 \(p\) 和 \(q\) 的相对熵 \(D(p \parallel q)\) 如下：

\[ D(p \parallel q) = \sum_{x \in \mathbb{X}}{p(x)\log \frac{p(x)}{q(x)}} \]

性质

熵和相对熵的性质很多，但现在我们只看证明“数据压缩极限”需要用到的一个性质：相对熵的非负性。

非负性

首先要证明一个不等式：Jensen 不等式。

Jensen 不等式描述如下：如果 \(f(x)\) 是凸函数，对于任意有限个 \(x\) 与 \(p\)，且 \(\sum{p_i}=1\)，有：

\[ f(\sum_{i=1}^{n}{p_i x_i}) \leq \sum_{i=1}^{n}{p_if(x_i)} \]

当 \(f\) 是严格凸函数时取等号。

考虑到 \(\sum{p_i}=1\)，这个命题其实就是在说：对于一个按 \(p(x)\) 分布的随机变量 \(X\) 和凸函数 \(f\)，有：

\[ f(E_{p(x)}[X]) \leq E_{p(x)}[f(X)] \]

考虑证明：

根据凸性的定义，任意一条弦都应该大于等于函数，则有：

\[ f(px_1 + (1-p)(x_2)) \leq pf(x_1) + (1-p)f(x_2) \]

结合图像会更好理解。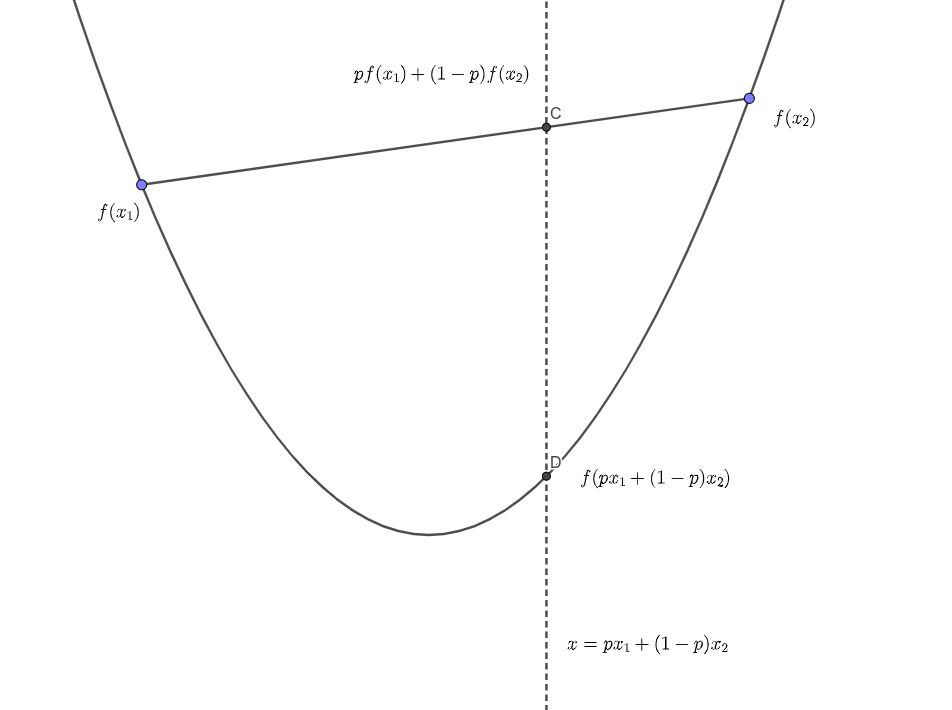

利用数学归纳法：假设当 \(n=k\) 时，Jensen 不等式成立，则有：

\[ f(\sum_{i=1}^{k}{p_i x_i}) \leq \sum_{i=1}^{k}{p_if(x_i)} \]

所以：

\[ \begin{aligned} f(\sum_{i=1}^{k+1}{p_i x_i}) &= f(p_{k+1}x_{k+1} + \sum_{i=1}^{k}{p_kx_k}) \\ &= f(p_{k+1}x_{k+1}+(1-p_{k+1})\sum_{i=1}^{k}{\frac{p_k}{1-p_{k+1}}x_k}) \\ & \leq p_{k+1}f(x_{k+1})+(1-p_{k+1})f(\sum_{i=1}^{k}{\frac{p_k}{1-p_{k+1}}x_k}) \\ & \leq p_{k+1}f(x_{k+1})+(1-p_{k+1})\sum_{i=1}^{k}{\frac{p_k}{1-p_{k+1}}f(x_i)} \\ &= \sum_{i=1}^{k+1}{p_if(x_i)} \end{aligned} \]

结合 \(n=2\) 时凸性的定义，Jensen 不等式成立。

利用 Jensen 不等式，就可以得到相对熵的非负性（注意到 \(\log\) 是凹函数，则 \(-\log\) 是凸函数）：

\[ \begin{aligned} D(p \parallel q) &= \sum_{x \in \mathbb{X}}{p(x)\log \frac{p(x)}{q(x)}} \\ &= \sum_{x \in \mathbb{X}}{p(x)(-\log \frac{q(x)}{p(x)})} \\ & \geq - \log(\sum_{x \in \mathbb{X}}{p(x) \frac{q(x)}{p(x)}}) \\ &= - \log(\sum_{x \in \mathbb{X}}{q(x)}) \\ &= - \log 1 \\ & \geq 0 \end{aligned} \]

信息压缩

终于来到了标题。我们现在知道的性质少得可怜——熵的绝大部分性质我都闭口不提。但是令人震惊的是，我们已经可以证明：熵是数据压缩的极限。

即时码

定义

现在你手上有一个随机变量 \(X\)，你不断地对 \(X\) 取值，并想把这些结果告诉别人。一个很自然的想法是，将 \(X\) 的所有可能结果都进行 \(D\) 进制编码（比如 ASCII 编码就是一个针对字符类型随机变量的二进制编码），然后将编码组成的字符串发送出去。

我们自然希望编码越短越好。具体来说，如果对于 \(X\) 的一个结果 \(x\)，其概率为 \(p(x)\)，而我们的编码是 \(C(x)\) ，长度是 \(l(x)\)，那么平均编码长度就是：\(L=\sum{p(x)l(x)}\) 。

我们希望最小化这个 \(L\)。但是 \(l(x)\) 是有一定限制的。首先显然有对于任意的 \(x_1 \neq x_2,C(x_1) \neq C(x_2)\)。但这还不够。比如我用 1010 表示 a，用 101 表示 b，用 010 表示 c。那么当连续的 101010101010 出现时，我们并不知道它说的是 aaa 还是 bcbc。

所以还有一条额外的要求：对于任意的 \(x_1 \neq x_2\)，\(C(x_1)\) 与 \(C(x_2)\) 都互不为对方的前缀。这样，当某种编码出现时，立刻就能知道它代表哪个信息，因为没有别的信息是它的前缀，它也不是别的信息的前缀。

满足这样的条件的编码方案，我们称为即时码，或者说前缀码。我们要找的，就是最优的前缀码。

性质

即时码的约束该如何转化为 \(l(x)\) 在数学上的约束呢？

根据我们的编码方案，我们建立一颗 \(D\) 叉字典树。假设最长的编码长度为 \(l_{max}\)，那么就建立一颗深度为 \(l_{max}\) 的满 \(D\) 叉字典树。（根节点深度为 0）

我们将所有的 \(C(x)\) 在字典树上对应的结束点标记出来，大概长这样：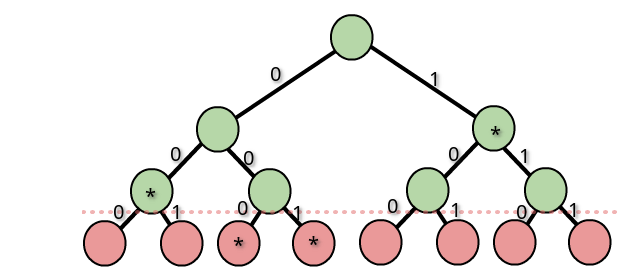

有什么用呢？由于每一个编码都不是其他编码的前缀，所以在一个结束标记的子树上，不可能有另一个结束标记。同样的，在它的祖先上也不会有结束标记。或者说，从任意一条由根节点到叶子节点的路径最多经过一个结束标记。

如果到达某个叶子节点的路径上经过了一个标记，我们就说这个标记“控制”了这个叶子节点。显然，不同的标记控制的节点没有重合。一个标记能控制几个叶子呢？如果这个标记对应的长度为 \(l(x)\)，那么它能控制 \(D^{L_{max} - l(x)}\) 个叶子节点。

又因为不同的标记控制的节点没有重合，且被控制的节点数小于等于总叶节点数，所以我们有：

\[ \begin{aligned} \sum_{x \in \mathbb{X}}{D^{l_{max} - l(x)}} & \leq D^{l_{max}} \\ \sum_{x \in \mathbb{X}}{D^{-l(x)}} & \leq 1 \end{aligned} \]

这被称为 Kraft 不等式。

我们已经证明了，即时码必须满足 Kraft 不等式。一组满足这个不等式的 \(l(x)\) 是不是一定可以构造成即时码呢？答案是肯定的，只要再做一遍建立字典树、分配叶子节点的工作就行了。（像哈夫曼编码的算法一样，将最长的两条编码放在相邻的子树里）

这样，我们就把编码问题变成了数学问题。

最后的问题

最优码长的下界

终于到了最后的证明。现在，问题已经变成了一个最优化问题：最小化 \(\sum{p(x)l(x)}\) 并满足 \(\sum{D^{-l(x)}} \leq 1\)。

使用扩展拉格朗日乘子法可以比较暴力地解决问题，不过有更简单的办法：

记 \(\sum{D^{-l(x)}} = c\)，先证明下界：

\[ \begin{aligned} \sum_{x \in \mathbb{X}}{p(x)l(x)} &= \sum_{x \in \mathbb{X}}{p(x)\log_D \frac{1}{D^{-l(x)}}} \\ &= \sum_{x \in \mathbb{X}}{p(x)\log_D \frac{p(x)}{D^{-l(x)}} - \log_D p(x)} \\ &= \sum_{x \in \mathbb{X}}{p(x)\log_D \frac{p(x)}{D^{-l(x)}}} + H(X) \\ &= \sum_{x \in \mathbb{X}}{p(x)\log_D \frac{p(x)}{\frac{D^{-l(x)}}{c}c}} + H(X) \\ &= \sum_{x \in \mathbb{X}}{p(x)\log_D \frac{p(x)}{\frac{D^{-l(x)}}{c}}} + H(X) - \log_D c \\ &= D(p \parallel \frac{D^{-l(x)}}{c}) + H(x) - \log_D c \\ & \geq H(X) \end{aligned} \]

由于 \(c \leq 1\)，所以 \(\log_D c \leq 0\)；再加上相对熵的非负性，我们就得到了 \(L\) 的下界。

容易得到，在 \(c=1\) 并且所有的 \(p(x)\) 都是 \(\frac{1}{D}\) 的整数幂的倍数时，这个下界是可以取得的。

最优码长的上界

我们已经知道，最优码长不可能短于 \(H(X)\)。但是，是不是所有的情况下最优码长都能达到 \(H(X)\) 呢？

我们采用构造的方法来证明：

对于任意一个概率分布 \(p\)，我们取 \(l(x) = \lceil -\log_D p(x)\rceil\)。先要确保满足 Kraft 不等式，才能保证一定存在这样的编码。这比较容易：

\[ \sum_{x \in \mathbb{X}}{D^{-l(x)}} = \sum_{x \in \mathbb{X}}{D^{-\lceil\log_D \frac{1}{p(x)}\rceil}} \leq \sum_{x \in \mathbb{X}}{D^{-\log_D \frac{1}{p(x)}}}=1 \]

那么有：

\[ -\log_D p(x) \leq l(x) < -\log_D p(x) + 1 \]

在两边对 \(X\) 取期望，得到：

\[ -\sum_{x \in \mathbb{X}}{p(x) \log_D p(x)} \leq -\sum_{x \in \mathbb{X}}{p(x) \log_D l(x)} < -\sum_{x \in \mathbb{X}}{p(x) \log_D p(x)} + 1 \]

即：

\[ H(X) \leq L < H(X) + 1 \]

现在我们知道，\(H(X)\) 是这一种编码的紧确界。由于最优码一定不会比我们构造的编码更差，所以有 \(H(X) \leq L^* < H(X) + 1\)。（\(L^*\) 表示最短编码的平均长度）

换句话说，\(L^* = \Theta(H(X))\)。

最优编码的构造

根据 Kraft 不等式构造的方法一点也不显然。幸运的是，简单易实现的 Huffman 编码正是一种最优码。

这个证明比较复杂，我们将其略去，转而关注另一个有意思的结果：最优进制。

最优的进制

从上面的分析可以看出，\(D\) 进制下编码的最优界为： \(-\sum{p(x)\log_D p(x)}\)。我们把这个长度记为 \(H_D(X)\)，即 \(D\) 进制下的熵。利用换底公式，我们得到 \(H_{D1}(X) = \frac{\ln D2}{\ln D1} H_{D2}(X)\)

显然 \(D\) 越大，\(H_D(X)\) 就越小。但是并不是 \(D\) 越大越好。因为从原理上来说，进制数越大，处理单个数据的硬件和软件就越复杂。如果处理单个数据需要 \(\Theta(D)=cD\) 的时间（\(c\) 为常数），那么实际的代价就是 \((cD)H_D(X)\)。

我们用 \(H_2(X)\) 为基准，则任何的 \(H_D(X)\) 都可以写成 \(\frac{\ln 2}{\ln D} H_2(X)\)

则总代价就是 \((cD)H_D(X) = cD\frac{\ln 2}{\ln D} H_2(X)\)。对它求导并让导数为 0，得到 \(D=e\)。这也就是我们常说的“\(e\) 进制最优”。

另一方面，\(\frac{3}{\ln 3} < \frac{2}{\ln 2}\)，所以才有“平衡三进制比二进制更优”的说法。