20220415题解
T1
题面描述
有 \(n\) 块冰霜石和 \(n\) 块猩红石,给出 \(m\) 个不组合关系 \((i, j)\) ,表示第 \(i\) 个猩红石和第 \(j\) 个冰霜石不能组合在一起。现在你希望将冰霜石和猩红石配对,以发挥他们的最大效用,求最多可以将几对冰霜石和猩红石配对成功?
思路
Cms大佬说可以拿网络流骗分呢!
但是显然网络流不可能是我们这种蒟蒻打的模拟赛的T1的正解。
所以考虑面向数据编程:
注意到每一个点的 \(n\) 和 \(m\) 都是固定的,并且有 \(m < 2n\) ,所以可以从这一方面入手:
我们记录每一个猩红石和哪一些冰霜石不能组合,存在一个 vector 里(就叫 a 吧)。
- 如果猩红石 \(i\) 满足
a[i].size()\(= n\) ,就是说它和所有的冰霜石都不能组合,答案一定是 \(n - 1\) 。因为剩下的不组合关系不超过 \(n - 1\) 个,不可能再把另一块猩红石堵死。 - 如果存在两块猩红石 \(i,j\),满足
a[i].size()\(=\)a[j].size()\(=n-1\) ,并且a[i]和a[j]完全相同,则说明满足 \(i\) 和满足 \(j\) 产生了冲突,必然要舍弃一个,答案也为 \(n - 1\) ,因为剩下的不组合关系最多有一个,不可能再产生影响。 - 如果前两组情况都不存在,答案就是 \(n\)
然后你就漂亮的 WA 了。
为什么呢?
我们只考虑了猩红石能不能配对,但是冰霜石他也应该拥有姓名。所以我们再记录每一个冰霜石和哪一些猩红石不能组合,也存在一个 vector 里(就叫 b 吧)。
然后如法炮制,也有3种情况。
最后安利一下 goto 的用法:1
2
3
4/*......*/
goto tags; //"tags" can be any name
/*......*/ //这些不会运行
tags: /*...*/ //会跳过上面的,直接执行这一行
这个关键字对于像本题这样发现一种情况之后直接结束的情况可以减少很多代码(即可以快速跳出深层循环)
AC代码
1 |
|
T3
题面描述
这是一个树上问题:
给你一棵树,从根节点出发,每次按照如下规则走:
- 如果当前点是叶子节点,那么可以返回自己的任意一个与自己距离不超过 \(k\) 的祖先。
- 如果当前节点不是叶子节点,那么可以访问自己的任意一个儿子节点。
问你最多可以访问多少个叶子节点。
思路
看完了题就感觉可以直接 dfs (没有这种感觉的请忽略)。
在yy了一会之后,想到可以把问题拆成两个部分:能回到根节点的叶子结点数 \(ans1\) 加上回不到根节点、但是能访问到的最多的叶子节点数 \(ans2\) 。对于每一个节点都把这两个玩意求出来,就是一个递归处理的过程。重点在于:已知每一个儿子节点的数据时,怎么把当前节点的数据算出来?
我们先考虑一个问题:怎么样的点是回不到根的?
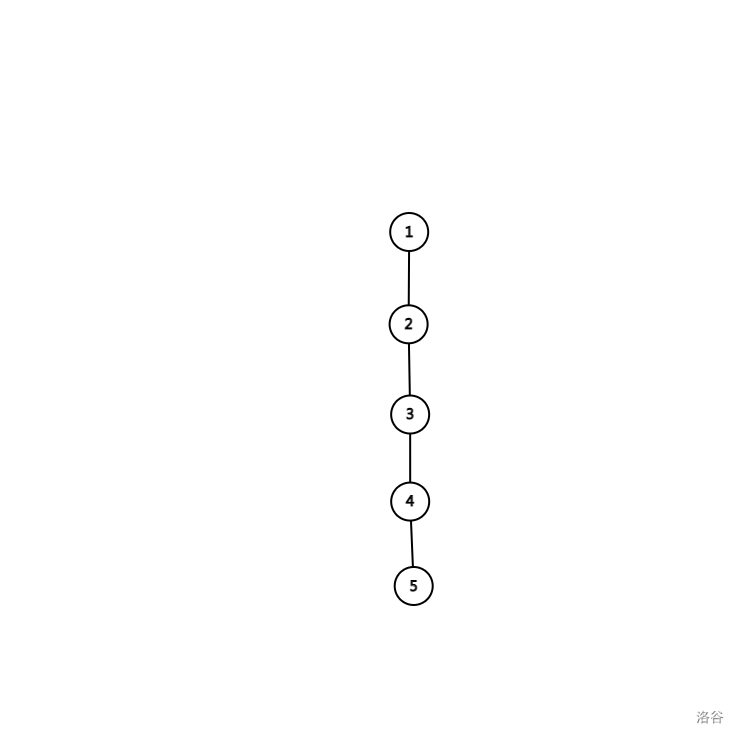
如图,在 \(k=3\) 的情况下,节点 \(5\) 是回不到根的。
但如果是下图情况:
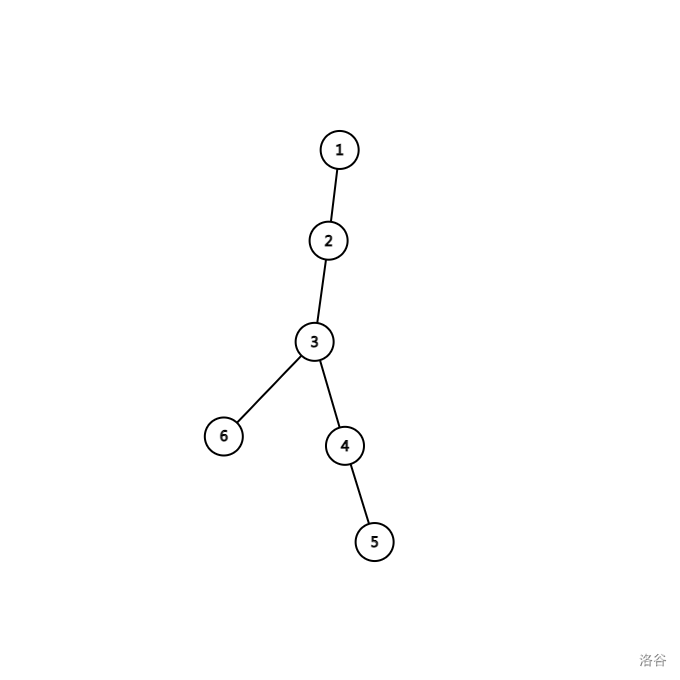
节点 \(5\) 可以通过 \(5 \to 3 \to 6 \to 1\) 的方式回到根啦!
基于上图的启发,我们再维护这样一个东西: \(dis_i\) 表示以 \(i\) 为根的子树中到 \(i\) 的距离最小的子节点到 \(i\) 的距离。现在,关键来了:
如果 \(u\) 是 \(v\) 的父亲,且 \(dis_v < k\) ,那么所有能回到 \(v\) 的子节点都一定能回到 \(u\) 。
根据这个,如果 \(dis_v < k\) ,那么 \(ans1_u\) += \(ans1_v\) 。如果 \(dis_v \ge k\) ,那么 \(ans1_v\) 对 \(ans1_u\) 没有贡献。
接下来考虑 \(ans2\) 。如果 \(dis_v < k\) ,那么回不到 \(v\) 的节点才是回不到 \(u\) 的, \(ans2_u = max(ans2_u, ans2_v)\) 。如果 \(dis_v \ge k\) ,那么无论回不回的到 \(v\) 的节点,都是回不到 \(u\) 的。此时如果最后决定走到 \(v\) ,那么既可以走的完 \(ans1_v\) , 还可以再走 \(ans2_v\) ,则 \(ans2_u = max(ans2_u, ans1_v + ans2_v)\) 。
AC代码
1 |
|